
【题目】如图,在ABC中,AB=AC=6![]() ,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.

【答案】![]() 或
或![]()
【解析】
过点A作AG⊥BC,垂足为G,根据等腰直角三角形的性质可得AG=BG=CG=6,设BD=x,则DF=BD=x,EF=7-x,然后利用勾股定理可得到关于x的方程,从而求得DG的长,继而可求得AD的长.
如图所示,过点A作AG⊥BC,垂足为G,
∵AB=AC=6![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=![]() =12,
=12,
∵AB=AC,AG⊥BC,
∴AG=BG=CG=6,
设BD=x,则EC=12-DE-BD=12-5-x=7-x,
由翻折的性质可知:∠DFA=∠B=∠C=∠AFE=45°,DB=DF,EF=FC,
∴DF=x,EF=7-x,
在Rt△DEF中,DE2=DF2+EF2,即25=x2+(7-x)2,
解得:x=3或x=4,
当BD=3时,DG=3,AD=![]() ,
,
当BD=4时,DG=2,AD=![]() ,
,
∴AD的长为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把二元一次方程![]() 的一个解用一个点表示出来,例如:可以把它的其中一个解
的一个解用一个点表示出来,例如:可以把它的其中一个解![]() 用点(2,1 )在平面直角坐标系中表示出来
用点(2,1 )在平面直角坐标系中表示出来
探究1:
(1)请你在直角坐标系中标出4个以方程![]() 的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
在这条直线上任取一点,这个点的坐标是方程![]() 的解吗? (填“是”或“不是”___
的解吗? (填“是”或“不是”___
(2)以方程![]() 的解为坐标的点的全体叫做方程
的解为坐标的点的全体叫做方程![]() 的图象.根据上面的探究想一想:方程
的图象.根据上面的探究想一想:方程![]() 的图象是_ _.
的图象是_ _.

探究2:根据上述探究结论,在同-平面直角坐标系中画出二元一次方程组![]() 中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组
中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组![]() 的解,即
的解,即
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BE平分∠ABC,交AD于点E、F是BC上一点,且CF=AE,连接DF.
(1)求证:四边形BEDF是平行四边形;
(2)若∠ABC=70°,求∠CDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州长江三桥于2019年5月30日建成通车,三桥如一架巨大的竖琴屹立于平湖之上,巍峨挺拔,绚丽多彩,成为万州靓丽的风景。周末,小明和爷爷一同在大桥上匀速散步,他们散步的速度是50米/分,小明观察到同向车道上驶过的公交车间隔时间是10分钟40秒,假定同向的公交车都保持48千米/小时的速度匀速行驶(中途停靠站的时间忽略不计),且公交车从车站发车的时间间隔是固定的,则车站每隔______分钟发出一辆公交车。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖的长方体盒子,如果这个无盖的长方体底面积为160cm2,那么该长方体盒子体积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,正方形![]() 的两边分别在正方形
的两边分别在正方形![]() 的边
的边![]() 和
和![]() 上,连接
上,连接![]() .填空:线段
.填空:线段![]() 与
与![]() 的数量关系为________;直线
的数量关系为________;直线![]() 与
与![]() 所夹锐角的大小为________.
所夹锐角的大小为________.



(2)如图②,将正方形![]() 绕点
绕点![]() 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
(3)把图②中的正方形都换成菱形,且![]() ,如图③,直接写出
,如图③,直接写出![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,为此某校从14 000名学生中随机抽取了200名学生就安全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图甲).
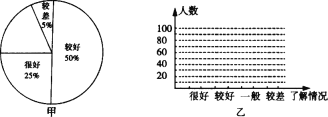
(1)补全扇形统计图,并计算这200名学生中对安全知识了解“较好”、“很好”的总人数;
(2)在图乙中,绘制样本频数的条形统计图;
(3)根据以上信息,请提出一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com