练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解方程：

    （1）x2+6x+5=0　（配方法）　

    （2）x2﹣1=2（x+1）（因式分解法）

    （3）2x2+3=6x （公式法）

    【答案】（1）x1=﹣1，x2=﹣5；（2）x1=﹣1，x2=3；（3）x1=，x2=．

    【解析】

    （1）根据配方法运算，可得答案；
    （2）根据因式分解运算，可得答案；
    （3）根据公式法运算，可得答案．

    （1）移项，得

    x2+6x=﹣5，

    配方，得

    （x+3）2=4，

    开方，得

    x+3=±2，

    x1=﹣1，x2=﹣5；

    （2）化简，得

    （x2﹣1）﹣2（x+1）=0，

    因式分解，得

    （x+1）（x﹣3）=0，

    于是，得

    x+1=0或x﹣3=0，

    解得x1=﹣1，x2=3；

    （3）化简，得

    2x2﹣6x+3=0

    a=2，b=﹣6，c=3，

    △=b2﹣4ac=36﹣4×2×3=12，

    x===，

    x1=，x2=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC和△DEF中，AB＝DE，∠A＝∠D，要使△ABC≌△DEF，必须增加的一个条件是_____(填写一个即可)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数的图象与x轴相交于A（﹣3，0）、B（1，0）两点，与y轴相交于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．

    （1）求D点坐标；

    （2）求二次函数的解析式；

    （3）根据图象直接写出使一次函数值小于二次函数值的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A=72°，∠BCD=31°，CD平分∠ACB．

    （1）求∠B的度数；

    （2）求∠ADC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，∠CAB=36°，以C为原点，C所在直线为y轴，BC所在直线为x轴建立平面直角坐标系 ，在坐标轴上取一点M使△MAB 为等腰三角形，符合条件的 M 点有（ ）

    A.6个B.7个

    C.8个D.9个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数y=的图象的一支位于第一象限，点A（x1，y1），B（x2，y2）都在该函数的图象上．

    （1）m的取值范围是　 　，函数图象的另一支位于第一象限，若x1＞x2，y1＞y2，则点B在第　 　象限；

    （2）如图，O为坐标原点，点A在该反比例函数位于第一象限的图象上，点C与点A关于x轴对称，若△OAC的面积为6，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

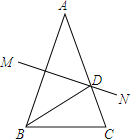
    【题目】如图，已知AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D.

    (1)求∠DBC的度数.

    (2)若△DBC的周长为14cm，BC＝5cm，求AB的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形OABC的顶点A(-8，0)、C(0，6)，点D是BC边上的中点，抛物线y=ax2+bx经过A、D两点，如图所示.

    (1)求点D关于y轴的对称点D′的坐标及a、b的值；

    (2)在y轴上取一点P,使PA+PD长度最短,求点P的坐标；

    (3)将抛物线y=ax2+bx向下平移,记平移后点A的对应点为A1，点D的对应点为D1，当抛物线平移到某个位置时，恰好使得点O是y轴上到A1、D1两点距离之和OA1+OD1最短的一点，求此抛物线的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店以固定进价一次性购进一种商品，3月份按一定售价销售，销售额为2400元，为扩大销量，减少库存，4月份在3月份售价基础上打9折销售，结果销售量增加30件，销售额增加840元．

    （1）求该商店3月份这种商品的售价是多少元？

    （2）如果该商店3月份销售这种商品的利润为900元，那么该商店4月份销售这种商品的利润是多少元？

    查看答案和解析>>

    同步练习册答案