
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4),(1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.

【答案】(1)y=﹣x2+3x+4;(2)M的坐标为(2,6).
【解析】
(1)由平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,且点A的坐标是(0,4),可求得点A′的坐标,然后利用待定系数法即可求得经过点C、A、A′的抛物线的解析式;
(2)首先连接AA′,设直线AA′的解析式为:y=kx+b,利用待定系数法即可求得直线AA′的解析式,再设点M的坐标为:(x,-x2+3x+4),继而可得△AMA′的面积,继而求得答案.
(1)∵平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,且点A的坐标是(0,4),
∴点A′的坐标为:(4,0),
∵点A、C的坐标分别是(0,4)、(﹣1,0),抛物线经过点C、A、A′,
设抛物线的解析式为:y=ax2+bx+c,
∴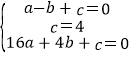 ,解得:
,解得: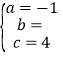 ,
,
∴此抛物线的解析式为:y=﹣x2+3x+4;
(2)连接AA′,设直线AA′的解析式为:y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线AA′的解析式为:y=﹣x+4,
设点M的坐标为:(x,﹣x2+3x+4),
则S△AMA′=![]() ×4×[﹣x2+3x+4﹣(﹣x+4)]=﹣2x2+8x=﹣2(x﹣2)2+8,
×4×[﹣x2+3x+4﹣(﹣x+4)]=﹣2x2+8x=﹣2(x﹣2)2+8,
∴当x=2时,△AMA′的面积最大,最大值S△AMA′=8,
∴M的坐标为:(2,6);


科目:初中数学 来源: 题型:
【题目】已知△ABC.
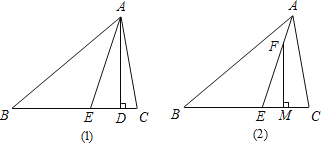
(1)如图(1),∠C>∠B,若 AD⊥BC 于点 D,AE 平分∠BAC,你能找出∠EAD 与∠B,∠C 之间的数量关系吗?并说明理由.
(2)如图(2),AE 平分∠BAC,F 为 AE 上一点,FM⊥BC 于点 M,∠EFM 与∠B,∠C之间有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④![]() 其中,正确的 是( )
其中,正确的 是( )

A.只有①②B.只有①②③C.只有③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE等于多少;
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.则AD与BE的数量关系为 ;∠AEB的度数为 度.
(2)拓展探究:如图2,如果△ACB和△CDE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,判断线段AE与BE的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
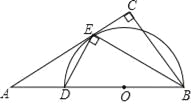
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=2![]() ,AE=6,求EC的长.
,AE=6,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
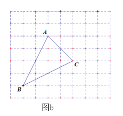
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
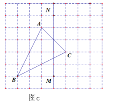
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com