
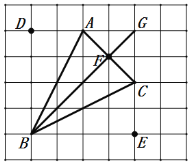
【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
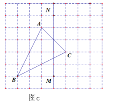
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
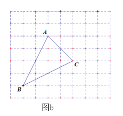
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析,理由见解析.
【解析】
(1)根据轴对称的性质及方格的特点,分别作出A、B、C关于直线MN的对称点![]() ,再顺次连接即可;
,再顺次连接即可;
(2)根据方格的特点,利用三角形面积公式把面积分三等份即可;
(3)根据方格的特点以及全等三角形的判定和性质,利用线段垂直平分线的定义求解.
(1)如图,△A′B′C′为所求作;
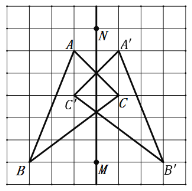
(2)如图,取格点O,计算可知S△AOC=S△BOC=S△AOB=2(平方单位)
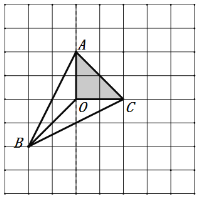
(3)如图,选择格点D、E,证明△ABD≌△CBE.于是,AB=CB.
选择格点Q,证明△ABQ≌△CBQ,于是,AQ=CQ.
∴BQ为线段AC的垂直平分线,
设BQ与AC相交于点F,则BF为所要求的△ABC的边AC上的高.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4),(1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形OACB为长方形,A(﹣6,0),B(0,4),直线l为函数y=﹣2x﹣5的图象.
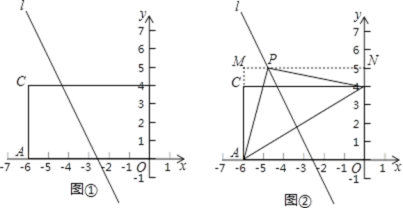
(1)点C的坐标为 ;
(2)若点P在直线l上,△APB为等腰直角三角形,∠APB=90°,求点P的坐标;
小明的思考过程如下:
第一步:添加辅助线,如图②,过点P作MN∥x轴,与y轴交于点N,与AC的延长线交于点M;
第二步:证明△MPA≌△NBP;
第三步:设NB=m,列出关于m的方程,进而求得点P的坐标.
请你根据小明的思考过程,写出第二步和第三步的完整解答过程;
(3)若点P在直线l上,点Q在线段AC上(不与点A重合),△QPB为等腰直角三角形,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型建立)
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)① 已知直线l1:y=![]() x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45
x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45![]() 至直线l2,如图2,求直线l2的函数表达式;
至直线l2,如图2,求直线l2的函数表达式;
② 如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-3x+6上的动点且在y轴的右侧.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察发现:如图(1),![]() 是
是![]() 的外接圆,点
的外接圆,点![]() 是边
是边![]() 上的一点,且
上的一点,且![]() 是等边三角形.
是等边三角形.![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 为圆心、
为圆心、![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)![]() _____;
_____;
(2)线段![]() 、
、![]() 有何大小关系?证明你的猜想.
有何大小关系?证明你的猜想.
拓展应用:如图(2),![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 延长线上的一点.点
延长线上的一点.点![]() 是
是![]() 的外接圆圆心,
的外接圆圆心,![]() 与
与![]() 相交于点
相交于点![]() .如果等边三角形
.如果等边三角形![]() 的边长为2,请直接写出
的边长为2,请直接写出![]() 的最小值和此时
的最小值和此时![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com