
【题目】(模型建立)
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)① 已知直线l1:y=![]() x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45
x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45![]() 至直线l2,如图2,求直线l2的函数表达式;
至直线l2,如图2,求直线l2的函数表达式;
② 如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-3x+6上的动点且在y轴的右侧.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.

【答案】(1)证明见解析;(2)①y=-7x-42;② (2,0)或(5,-9)
【解析】
(1)根据△ABC为等腰直角三角形,AD⊥ED,BE⊥ED,可判定△ACD≌△CBE;
(2)①过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,根据△CBD≌△BAO,得出BD=AO=6,CD=OB=8,求得C(-8,14),最后运用待定系数法求直线l2的函数表达式;②根据△APD是以点D为直角顶点的等腰直角三角形,当点D是直线y=-3x+6上的动点且在y轴的右侧时,分两种情况:当点D在矩形AOCB的内部或边上时,当点D在矩形AOCB的外部时,设D(x,-3x+6),分别根据△ADE≌△DPF,得出AE=DF,据此列出方程进行求解即可.
解:(1)证明:如图1,∵△ABC为等腰直角三角形,
∴CB=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,
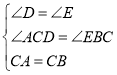
∴△ACD≌△CBE(AAS);
(2)①如图2,过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,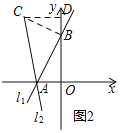
∵∠BAC=45°,
∴△ABC为等腰直角三角形,
由(1)可知:△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=![]() x+8中,若y=0,则x=-6;若x=0,则y=8,
x+8中,若y=0,则x=-6;若x=0,则y=8,
∴A(-6,0),B(0,8),
∴BD=AO=6,CD=OB=8,
∴OD=8+6=14,
∴C(-8,14),
设l2的解析式为y=kx+b,则
![]()
解得![]()
∴l2的解析式:y=-7x-42;
②D(2,0),(5,-9)
理由:当点D是直线y=-3x+6上的动点且在y轴右侧时时,分两种情况:
当点D在矩形AOCB的内部或边上时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F, 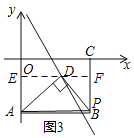
设D(x,-3x+6),则OE=3x-6,AE=6-(3x-6)=12-3x,DF=EF-DE=8-x,
由(1)可得,△ADE≌△DPF,则DF=AE,
即:12-3x=8-x,
解得2x=4,x=2,
∴-3x+6=0,
∴D(2,0),即点D为直线y=-3x+6与x轴交点,
此时,PF(PC)=ED(OD)=2,AO=6=CD,符合题意;
准确图形如下: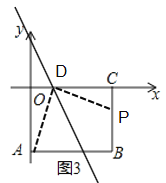
当点D在矩形AOCB的外部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F, 
设D(x,-3x+6),则OE=3x-6,AE=OE-OA=3x-6-6=3x-12,DF=EF-DE=8-x,
同理可得:△ADE≌△DPF,则AE=DF,
即:3x-12=8-x,
解得x=5,
∴-3x+6=-9,
∴D(5,-9),
此时,ED=PF=5,AE=BF=DF=3,BP=PF-BF=5-3=2 <6,点P在线段BC上,符合题意.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.则AD与BE的数量关系为 ;∠AEB的度数为 度.
(2)拓展探究:如图2,如果△ACB和△CDE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,判断线段AE与BE的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
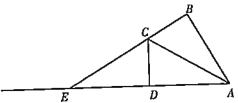

(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .设
.设![]() ,点
,点![]() 是直线
是直线![]() 上的动点,当
上的动点,当![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 是否可能重合?若可能,请说明理由并求此时
是否可能重合?若可能,请说明理由并求此时![]() 的值(用含
的值(用含![]() 的式子表示);若不可能,请说明理由.
的式子表示);若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )

A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
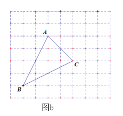
【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
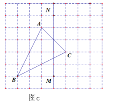
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O分别交BC、AC于F、G,且G是![]() 的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
(1)求证:DE是的⊙O切线;
(2)若AB=6,BG=4,求BE的长;
(3)若AB=6,CE=1.2,请直接写出AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com