
【题目】如图,以△ABC的边AB为直径的⊙O分别交BC、AC于F、G,且G是![]() 的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
(1)求证:DE是的⊙O切线;
(2)若AB=6,BG=4,求BE的长;
(3)若AB=6,CE=1.2,请直接写出AD的长.

【答案】(1)证明见解析;(2)![]() ;(3)2.
;(3)2.
【解析】
(1)要证明DE是的⊙O切线,证明OG⊥DE即可;
(2)先证明△GBA∽△EBG,即可得出![]() =
=![]() ,根据已知条件即可求出BE;
,根据已知条件即可求出BE;
(3)先证明△AGB≌△CGB,得出BC=AB=6,BE=4.8再根据OG∥BE得出![]() =
=![]() ,即可计算出AD.
,即可计算出AD.
证明:(1)如图,连接OG,GB,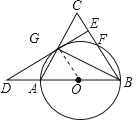
∵G是弧AF的中点,
∴∠GBF=∠GBA,
∵OB=OG,
∴∠OBG=∠OGB,
∴∠GBF=∠OGB,
∴OG∥BC,
∴∠OGD=∠GEB,
∵DE⊥CB,
∴∠GEB=90°,
∴∠OGD=90°,
即OG⊥DE且G为半径外端,
∴DE为⊙O切线;
(2)∵AB为⊙O直径,
∴∠AGB=90°,
∴∠AGB=∠GEB,且∠GBA=∠GBE,
∴△GBA∽△EBG,
∴![]() ,
,
∴![]() ;
;
(3)AD=2,根据SAS可知△AGB≌△CGB,
则BC=AB=6,
∴BE=4.8,
∵OG∥BE,
∴![]() ,即
,即![]() ,
,
解得:AD=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(模型建立)
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)① 已知直线l1:y=![]() x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45
x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45![]() 至直线l2,如图2,求直线l2的函数表达式;
至直线l2,如图2,求直线l2的函数表达式;
② 如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-3x+6上的动点且在y轴的右侧.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )

A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
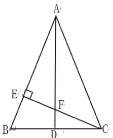
【题目】如图,AD为△ABC的中线,AB=AC,∠BAC=45.过点C 作CE⊥AB,垂足为E,CE与AD交于点F.
(1)求证: △AEF≌△CEB;
(2)试探索AF与CD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 、
、![]() 是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在
是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在![]() 、
、![]() 两处分别与道路相切),测得
两处分别与道路相切),测得![]() 米,
米,![]() .
.
![]() 在图中画出圆弧形弯道的示意图(用尺规作图,保留作图痕迹,不写作法与证明);
在图中画出圆弧形弯道的示意图(用尺规作图,保留作图痕迹,不写作法与证明);
![]() 计算弯道部分的长度(结果用
计算弯道部分的长度(结果用![]() 表示并保留根号).
表示并保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com