【题目】如图
、
是两条垂直的公路，设计时想在拐弯处用一段圆弧形弯道把它们连接起来（圆弧在
、
两处分别与道路相切），测得
米，
．
在图中画出圆弧形弯道的示意图（用尺规作图，保留作图痕迹，不写作法与证明）；
计算弯道部分的长度（结果用
表示并保留根号）．
科目：初中数学 来源： 题型：
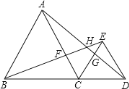
【题目】如图，以△ABC的边AB为直径的⊙O分别交BC、AC于F、G，且G是
的中点，过点G作DE⊥BC，垂足为E，交BA的延长线于点D
（1）求证：DE是的⊙O切线；
（2）若AB=6，BG=4，求BE的长；
（3）若AB=6，CE=1.2，请直接写出AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，是瑞安部分街道示意图，
，
，
，
，
，
，
，
，
，
为“公交汽车”停靠点，甲公共汽车从站出发，按照，，，，，，的顺序到达站，乙公共汽车从站出发，按照，，，，，，的顺序到达站，如果甲、乙两车分别从、两站同时出发，各站耽误的时间相同，两辆车速度也一样，则（ ）
A. 甲车先到达指定站 B. 乙车先到达指定站
C. 同时到达指定站 D. 无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC分别沿AB，AC翻折得到△ABD 和△AEC，线段BD与AE交于点 F，连接BE .
（1）如果∠ABC=16，∠ACB=30°，求∠DAE的度数；
（2）如果BD⊥CE，求∠CAB 的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
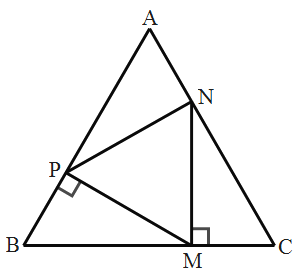
【题目】如图，点P、M、N分别在等边△ABC的各边上，且MP⊥AB于点P，MN⊥BC于点M，PV⊥AC于点N，若AB＝12cm，求CM的长为______cm.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】建立模型：
如图1，等腰Rt△ABC中，∠ABC＝90°，CB＝BA，直线ED经过点B，过A作AD⊥ED于D，过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角，所以在平面直角坐标系中被大量使用.
模型应用：
(1)如图2，点A（0，4)，点B(3，0），△ABC是等腰直角三角形．
①若∠ABC＝90°，且点C在第一象限，求点C的坐标；
②若AB为直角边，求点C的坐标；
(2)如图3，长方形MFNO，O为坐标原点，F的坐标为（8，6），M、N分别在坐标轴上，P是线段NF上动点，设PN＝n，已知点G在第一象限，且是直线y＝2x一6上的一点，若△MPG是以G为直角顶点的等腰直角三角形，请直接写出点G的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABO中，∠OBA=90°，AB=OB，点C在边AB上，且C(6，4)，点D为OB的中点，点P为边OA上的动点，当∠APC=∠DPO时，点P的坐标为 ____.
查看答案和解析>>
科目：初中数学 来源： 题型：
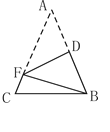
【题目】如图，在△ABC中，AB="AC," AB＋BC=8．将△ABC折叠，使得点A落在点B处，折痕DF分别与AB、AC交于点D、F，连接BF，则△BCF的周长是（ ）
A.8B.16C.4D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
