
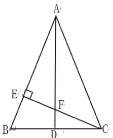
【题目】如图,AD为△ABC的中线,AB=AC,∠BAC=45.过点C 作CE⊥AB,垂足为E,CE与AD交于点F.
(1)求证: △AEF≌△CEB;
(2)试探索AF与CD的数量关系,并说明理由.
【答案】(1) 见解析;(2) ![]() ,理由见解析
,理由见解析
【解析】
(1)根据三线合一可得:![]() ,AD⊥BC,从而得出∠ADB=90°,然后根据等腰直角三角形的判定,可得△AEC为等腰直角三角形,从而得出AE=CE,再根据同角的余角相等可得∠BAD =∠ECB,最后利用ASA即可证出△AEF≌△CEB;
,AD⊥BC,从而得出∠ADB=90°,然后根据等腰直角三角形的判定,可得△AEC为等腰直角三角形,从而得出AE=CE,再根据同角的余角相等可得∠BAD =∠ECB,最后利用ASA即可证出△AEF≌△CEB;
(2)根据全等三角形的性质可得:AF=CB,从而得出![]() .
.
解:(1)∵AD为△ABC的中线,AB=AC,
∴![]() ,AD⊥BC,
,AD⊥BC,
∴∠ADB=90°
∴∠BAD+∠B=90°
∵CE⊥AB,∠BAC=45
∴∠BEC=∠FEA=90°,△AEC为等腰直角三角形
∴∠ECB+∠B=90°,AE=CE
∴∠BAD =∠ECB
在△AEF和△CEB中
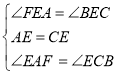
∴△AEF≌△CEB;
(2)![]() ,理由如下:
,理由如下:
∵△AEF≌△CEB
∴AF=CB
∵![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )

A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
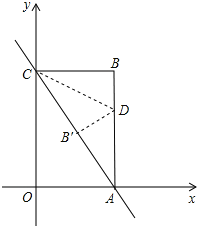
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O分别交BC、AC于F、G,且G是![]() 的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
(1)求证:DE是的⊙O切线;
(2)若AB=6,BG=4,求BE的长;
(3)若AB=6,CE=1.2,请直接写出AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,直线![]() 分别交
分别交![]() 轴
轴![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 的长满足
的长满足![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() .
.

![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 求过点
求过点![]() 的反比例函数解析式;
的反比例函数解析式;
![]() 点
点![]() 在反比例函数图象上是否存在一点
在反比例函数图象上是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形?若存在,请直接写出点
为腰的四边形为梯形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC分别沿AB,AC翻折得到△ABD 和△AEC,线段BD与AE交于点 F,连接BE .
(1)如果∠ABC=16,∠ACB=30°,求∠DAE的度数;
(2)如果BD⊥CE,求∠CAB 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com