
【题目】如图,已知,直线![]() 分别交
分别交![]() 轴
轴![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 的长满足
的长满足![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() .
.

![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 求过点
求过点![]() 的反比例函数解析式;
的反比例函数解析式;
![]() 点
点![]() 在反比例函数图象上是否存在一点
在反比例函数图象上是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形?若存在,请直接写出点
为腰的四边形为梯形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】![]() ;
;![]() ;
;![]() 的坐标是
的坐标是![]() .
.
【解析】
(1)根据非负数的性质求得OA和OB的长,即A和B的坐标,利用待定系数法求得直线l的解析式;
(2)AP=2BP,则AB=BP,作PE⊥y轴于点E,证明△AOB≌△PEB,求得PE和OE的长,则P的坐标即可求得,然后利用待定系数法求得反比例函数解析式;
(3)点A、B、C、D为顶点,AC为腰的四边形为梯形,则是梯形ABDC,其中D在第四象限,求得CD的解析式,然后解直线CD的解析式和反比例函数解析式的交点即可求解.
![]() ∵
∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
则![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ,
,
设直线![]() 的解析式是
的解析式是![]() ,根据题意得:
,根据题意得:![]() ,
,
解得: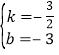 ,
,
则直线![]() 的解析式是
的解析式是![]() ;
;
![]() ∵
∵![]() ,
,
∴![]() ,
,
作![]() 轴于点
轴于点![]() .
.
在![]() 和
和![]() 中,
中,
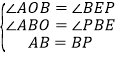 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
∴![]() 的坐标是
的坐标是![]() .
.
设反比例函数的解析式是![]() ,把
,把![]() 代入得:
代入得:![]() ,
,
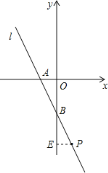
则反比例函数的解析式是:![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形,
为腰的四边形为梯形,
则是梯形![]() ,其中
,其中![]() 在第四象限.
在第四象限.
设直线![]() 的解析式是
的解析式是![]() ,把
,把![]() 代入解析式得:
代入解析式得:![]() ,
,
解得:![]() ,
,
则直线![]() 的解析式是:
的解析式是:![]() .
.
解方程组 ,
,
解得:![]() 或
或![]() (舍去).
(舍去).
则![]() 的坐标是
的坐标是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,AB=AC,∠BAC=45.过点C 作CE⊥AB,垂足为E,CE与AD交于点F.
(1)求证: △AEF≌△CEB;
(2)试探索AF与CD的数量关系,并说明理由.
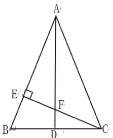
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 在反比例函数图象上,
在反比例函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
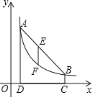
(1)求![]() ,
,![]() 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
![]() 求
求![]() 的长;
的长;
![]() 过点
过点![]() 作
作![]() ,交轴于点
,交轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,如果
的条件下,如果![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,设
,设![]() ,问是否存在这样的使得
,问是否存在这样的使得![]() 与
与![]() 相似?若存在,请求出的
相似?若存在,请求出的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,点A、B分别在边ON和OM上(∠OAB≠45°).

(1)根据要求,利用尺规作图,补全图形:
第①步:作∠MON的平分线OC,作线段AB的垂直平分线l,OC和l交于点P,第②步:连接PA、PB;
(2)结合补完整的图形,判断PA和PB有什么数量关系和位置关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com