
【题目】如图,点![]() ,
,![]() 在反比例函数图象上,
在反比例函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
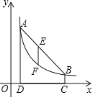
(1)求![]() ,
,![]() 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
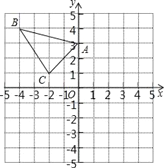
【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为![]() 的滑动变阻器及一电流表测电源电压,结果如图所示.
的滑动变阻器及一电流表测电源电压,结果如图所示.
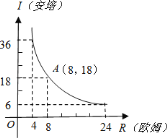
![]() 电流
电流![]() (安培)与电阻
(安培)与电阻![]() (欧姆)之间的函数解析式为________;
(欧姆)之间的函数解析式为________;
![]() 当电阻在
当电阻在![]() 之间时,电流应在________范围内,电流随电阻的增大而________;
之间时,电流应在________范围内,电流随电阻的增大而________;
![]() 若限制电流不超过
若限制电流不超过![]() 安培,则电阻在________之间.
安培,则电阻在________之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,直线![]() 分别交
分别交![]() 轴
轴![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 的长满足
的长满足![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() .
.

![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 求过点
求过点![]() 的反比例函数解析式;
的反比例函数解析式;
![]() 点
点![]() 在反比例函数图象上是否存在一点
在反比例函数图象上是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形?若存在,请直接写出点
为腰的四边形为梯形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是圆圆设计的“作等腰三角形一腰上的高线”的尺规作图过程 .
已知:△![]() ,
,![]() .
.
求作:![]() 边上的高线.
边上的高线.
作法:如图,

①以点![]() 为圆心,
为圆心,![]() 为半径画弧,交
为半径画弧,交![]() 于点
于点![]() 和点
和点![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点![]() ;
;
③作射线![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 就是所求作的
就是所求作的![]() 边上的高线.
边上的高线.
根据圆圆设计的尺规作图过程,完成下列问题:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵![]() ,
,
∴点![]() 在线段
在线段![]() 的垂直平分线上(__________) (填推理的依据).
的垂直平分线上(__________) (填推理的依据).
∵__________=__________,
∴点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
∴![]() 是线段
是线段![]() 的垂直平分线.
的垂直平分线.
∴![]() ⊥
⊥![]() .
.
∴线段![]() 就是
就是![]() 边上的高线.
边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题 .
已知 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….,当
,….,当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ;当
;当![]() 为大于1的偶数时,
为大于1的偶数时,![]() .
.
(1)求![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(2)直接写出![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(3)计算:![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,过点C作CE⊥CD,且CE=CD,连接DE交BC于点F,连接BE.
(1)求证:AB⊥BE;
(2)当AD=BF时,求∠BEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是_____.
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(4)OGBD=AE2+CF2.
;(4)OGBD=AE2+CF2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com