
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,过点C作CE⊥CD,且CE=CD,连接DE交BC于点F,连接BE.
(1)求证:AB⊥BE;
(2)当AD=BF时,求∠BEF的度数.

【答案】(1)证明见解析;(2)∠BEF=67.5°.
【解析】
(1)由等腰直角三角形的性质可得∠A=∠ABC=45°,根据“SAS”可证△ACD≌△BCE,可得∠A=∠CBE=45°=∠ABC,即AB⊥BE;
(2)由全等三角形的性质可得AD=BE=BF,根据等腰三角形的性质和三角形内角和定理可求∠BEF的度数.
证明:(1)∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∵CE⊥CD,
∴∠DCE=90°,
∴∠ACB=∠DCE,
∴∠ACD=∠BCE,且AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴∠A=∠CBE=45°,
∵∠ABE=∠ABC+∠CBE=45°+45°=90°,
∴AB⊥BE;
(2)∵△ACD≌△BCE,
∴AD=BE,
∵AD=BF,
∴BE=BF,且∠CBE=45°,
∴∠BEF=∠BFE=67.5°.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4![]() x+12+m=0.
x+12+m=0.
(1)若方程的一个根是![]() ,求m的值及方程的另一根;
,求m的值及方程的另一根;
(2)若方程的两根恰为等腰三角形的两腰,而这个三角形的底边为m,求m的值及这个等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为学校购买运动会的奖品后,回学校向后勤处赵主任交账说:我买了两种书共105本,单价分别为8元和12元,买书前我领了1600元,现在还余518元.赵主任算了一下说:你肯定搞错了.
(1)赵主任为什么说他搞错了,请你用方程组的知识给予解释;
(2)王老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,笔记本的单价可能为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
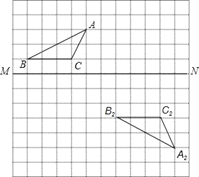
【题目】在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为创建“书香校园”,购置了一批图书,已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量与购买文学类图书的数量相等.求科普类图书平均每本的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,若存在一个内角角度,是另外一个内角角度的
中,若存在一个内角角度,是另外一个内角角度的![]() 倍(
倍(![]() 为大于1的正整数),则称
为大于1的正整数),则称![]() 为
为![]() 倍角三角形.例如,在
倍角三角形.例如,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,所以
,所以![]() 为3倍角三角形.
为3倍角三角形.
(1)在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 为________倍角三角形;
为________倍角三角形;
(2)若![]() 是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的
是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的![]() ,求
,求![]() 的最小内角.
的最小内角.
(3)若![]() 是2倍角三角形,且
是2倍角三角形,且![]() ,请直接写出
,请直接写出![]() 的最小内角的取值范围.
的最小内角的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
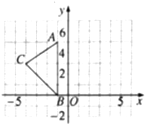
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com