
【题目】(1)问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.则AD与BE的数量关系为 ;∠AEB的度数为 度.
(2)拓展探究:如图2,如果△ACB和△CDE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,判断线段AE与BE的位置关系,并说明理由.

【答案】(1)相等,60;(2)AE⊥BE,理由见解析.
【解析】
(1)由条件△ACB和△DCE均为等边三角形,易证△ACD≌△BCE,从而得到对应边相等,即AD=BE;由△ACD≌△BCE,可得∠ADC=∠BEC,由点A,D,E在同一直线上,可求出∠ADC=120°,从而可以求出∠AEB的度数;
(2)首先根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°.
(1)∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∵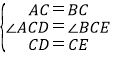 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°,
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=60°,
故答案为:相等,60;
(2)AE⊥BE,
∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
∵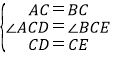 ,
,
∴△ACD≌△BCE(SAS),
∴BE=AD,∠BEC=∠ADC,
∵点A,D,E在同一直线上,
∴∠ADC=180-45=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°,即AE⊥BE.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
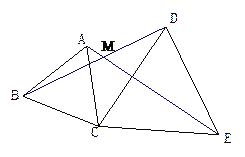
【题目】如图,把△ACE绕点C逆时针旋转60°后与△BCD重合,BD、AE.交于点 M,连接AB、DE.
(1)求证:△ABC和△CDE为等边三角形;
(2)求∠AMB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
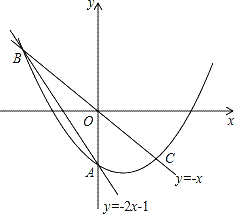
【题目】如图,在平面直角坐标系中,O为原点,直线y=2x﹣1,与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(1)求过A,B,C三点的抛物线的解析式;
(2)P为抛物线上一点,它关于原点的对称点为Q,当四边形PBQC为菱形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋中装有红、黄、绿三种颜色的球共36个,它们除颜色外都相同,其中黄球个数是绿球个数的2倍,已知从袋中摸出一个球是红球的概率为![]() .
.
(1)分别求红球和绿球的个数.
(2)求从袋中随机摸出一球是绿球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
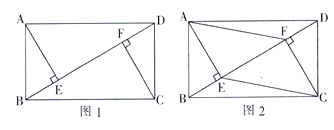
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() .
.![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | d |
八(2) | a | 85 | 85 | e |
(1)直接写出表中a,b,c的值:a= ,b= ,c= .
(2)求d,e的值,并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
(3)若“醴陵市中小学生首届诗词大会”中,各中学代表队成绩计分分两部分:现场评委记分和网络评委投票记分。且现场评委记分权数为80%,网络评委投票记分权数为20%,请计算A,B,C三所中学代表队的最终得分为多少?
中学A | 中学B | 中学C | |
评委记分 | 90 | 80 | 85 |
网络投票记分 | 85 | 92 | 88 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC,BE=BC.当∠CBE:∠BCE=_________,求证:四边形ABCD是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com