Question

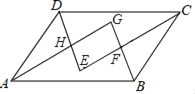
【题目】已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC，BE=BC．当∠CBE：∠BCE=_________，求证：四边形ABCD是正方形．

Answer 1

【答案】2：3，证明见解析．

【解析】

首先证得△ADE≌△CDE，由全等三角形的性质可得∠ADE=∠CDE，由AD∥BC可得∠ADE=∠CBD，可得∠CDB=∠CBD，可得BC=CD，可得AD=BC，利用平行四边形的判定定理可得四边形ABCD为平行四边形，由AD=CD可得四边形ABCD是菱形； 由BE=BC可得△BEC为等腰三角形，可得∠BCE=∠BEC，利用三角形的内角和定理可得∠CBE =45°，可得∠ABE=45°，可得∠ABC=90°，由正方形的判定定理可得四边形ABCD是正方形．

证明：当∠CBE：∠BCE=时，四边形ABCD是正方形．

理由如下：

在△ADE与△CDE中，

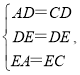
∴∠ADE=∠CDE，

∵AD∥BC，

∴∠ADE=∠CBD，

∴∠CDE=∠CBD，

∴BC=CD，

∵AD=CD，

∴BC=AD，

∴四边形ABCD为平行四边形，

∵AD=CD，

∴四边形ABCD是菱形；

∵BE=BC

∴∠BCE=∠BEC，

∵∠CBE：∠BCE=2：3，

∴∠CBE=180×=45°，

∵四边形ABCD是菱形，

∴∠ABE=45°，

∴∠ABC=90°，

∴四边形ABCD是正方形．