
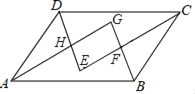
【题目】如图,在ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
【答案】(1)证明见解析;(2)矩形EFGH的面积=![]() .
.
【解析】
(1)根据角平分线的定义以及平行四边形的性质,即可得出∠AGB=90°,∠DEC=90°,∠AHD=90°=∠EHG,进而判定四边形EFGH是矩形;
(2)根据含30°角的直角三角形的性质,得到BG![]() AB=3,AG=3
AB=3,AG=3![]() CE,BF
CE,BF![]() BC=2,CF=2
BC=2,CF=2![]() ,进而得出EF和GF的长,可得四边形EFGH的面积.
,进而得出EF和GF的长,可得四边形EFGH的面积.
(1)∵GA平分∠BAD,GB平分∠ABC,∴∠GAB![]() ∠BAD,∠GBA
∠BAD,∠GBA![]() ∠ABC.
∠ABC.
∵ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA![]() (∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得:∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得:∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(2)依题意得:∠BAG![]() ∠BAD=30°.
∠BAD=30°.
∵AB=6,∴BG![]() AB=3,AG=3
AB=3,AG=3![]() CE.
CE.
∵BC=4,∠BCF![]() ∠BCD=30°,∴BF
∠BCD=30°,∴BF![]() BC=2,CF=2
BC=2,CF=2![]() ,∴EF=3
,∴EF=3![]() ,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF
,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF![]() .
.


科目:初中数学 来源: 题型:
【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
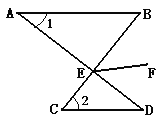
【题目】如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=300,∠2=400。(1)求∠B、∠D的度数.(2)求∠BEF的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC,BE=BC.当∠CBE:∠BCE=_________,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )

A.AB=BEB.BE⊥DCC.∠ABE=90°D.BE平分∠DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营一批进价2元的小商品,在经营中发现此商品的日销售单价与日销量之间的关系如表:
日销售单价(元) | 3 | 5 | 7 | 9 | 11 |
日销量(件) | 18 | 14 | 10 | 6 | 2 |
(1)上表反映了日销售单价与日销量之间的关系,其中 是自变量, 是因变量.
(2)如果用x表示日销售单价,y表示日销量,那么y与x之间的关系式是 ;
(3)日销售单价为 元时,商场日销售盈利最高?(盈利![]() 日销售总额-日销售商品的总进价)
日销售总额-日销售商品的总进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com