
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
【答案】(1)见解析;(2)∠BDF=18°.
【解析】
(1)先证明四边形ABCD是平行四边形,求出∠ABC=90°,然后根据矩形的判定定理,即可得到结论;
(2)求出∠FDC的度数,根据三角形的内角和,求出∠DCO,然后得到OD=OC,得到∠CDO,即可求出∠BDF的度数.
(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
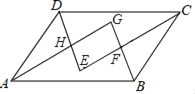
【题目】如图,在ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,下列四个结论中错误的是( )
,下列四个结论中错误的是( )
A.如果方程![]() 有两个不相等的实数根,那么方程
有两个不相等的实数根,那么方程![]() 也有两个不相等的实数
也有两个不相等的实数
B.如果4是方程![]() 的一个根,那么
的一个根,那么![]() 是方程
是方程![]() 的另一个根
的另一个根
C.如果方程![]() 有两根符号相同,那么方程
有两根符号相同,那么方程![]() 的两符号也相同
的两符号也相同
D.如果方程![]() 和方程
和方程![]() 有一个相同的根,那么这个根必是
有一个相同的根,那么这个根必是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则△DCE的面积为( )

A. ![]() B.
B. ![]() C. 2D. 1
C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,E到C时两点同时停止运动。设点E运动的时间为ts(![]() ).
).
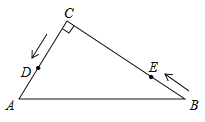
(1)AB=__________cm, CE=__________cm;
(2)当△BDE是直角三角形时,求t的值;
(3)若四边形CDEF是以CD、DE为一组邻边的平行四边形,
①设平行四边形CDEF的面积为Scm2,求S于t的关系式;
②是否存在某个时刻t,使□CDEF为菱形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点B,C分别是∠MAN的边AM、AN上的点,满足AB=BC,点P为射线的AB上的动点,点D为点B关于直线AC的对称点,连接PD交AC于E点,交BC于点F。
(1)在图1中补全图形;
(2)求证:∠ABE=∠EFC;
(3)当点P运动到满足PD⊥BE的位置时,在射线AC上取点Q,使得AE=EQ,此时![]() 是否是一个定值,若是请直接写出该定值,若不是,请说明理由.
是否是一个定值,若是请直接写出该定值,若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
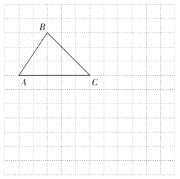
【题目】在平面直角坐标系xOy中,△ABC的三个顶点分别是A(-2,0),B(0,3),C(3,0).
(1)在所给的图中,画出这个平面直角坐标系;
(2)点A经过平移后对应点为D(3,-3),将△ABC作同样的平移得到△DEF,点B的对应点为点E,画出平移后的△DEF;
(3)在(2)的条件下,点M在直线CD上,若DM=2CM,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com