
【题目】已知△ABC.
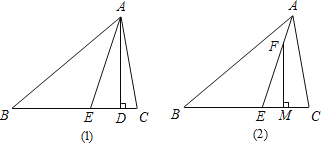
(1)如图(1),∠C>∠B,若 AD⊥BC 于点 D,AE 平分∠BAC,你能找出∠EAD 与∠B,∠C 之间的数量关系吗?并说明理由.
(2)如图(2),AE 平分∠BAC,F 为 AE 上一点,FM⊥BC 于点 M,∠EFM 与∠B,∠C之间有何数量关系?并说明理由.
【答案】(1)∠EAD=![]() (∠C-∠B);理由见解析;(2)∠EFM=
(∠C-∠B);理由见解析;(2)∠EFM= ![]() (∠C-∠B) ;理由见解析.
(∠C-∠B) ;理由见解析.
【解析】
(1)分析题意,观察图形可知∠EAD=∠EAC-∠DAC,即若用∠B、∠C分别表示出∠EAC、∠DAC即可;首先根据三角形内角和定理及角平分线的定义即可用∠B、∠C表示出∠EAV,再根据直角三角形两锐角互余可得∠DAC=90°-∠C,据此可解答;
对于(2)过点A作AD⊥BC于D,根据两直线平行,同位角相等可得∠EFM=∠EAD,再结合(1)的结论进行解答即可
解:(1)∵AE 平分∠BAC,
∴∠EAC=![]() ∠BAC=
∠BAC=![]() (180-∠B-∠C),
(180-∠B-∠C),
又∵AD⊥BC,
∴∠DAC=90-∠C,
∴∠EAD=∠EAC-∠DAC= ![]() (180-∠B-∠C)-(90-∠C)=
(180-∠B-∠C)-(90-∠C)= ![]() (∠C-∠B),
(∠C-∠B),
即∠EAD=![]() (∠C-∠B);·
(∠C-∠B);·
(2)如图,过点 A 作 AD⊥BC 于 D,
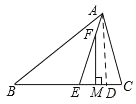
∵FM⊥BC,
∴AD∥FM,
∴∠EFM=∠EAD= ![]() (∠C-∠B)
(∠C-∠B)


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数 | 一次项系数 | 常数项 | |
(2x + l)(x + 2) | 2 | 2 | |
(2x + 1)(3x - 2) | 6 | -2 | |
(ax + b)( mx + n) | am | bn |
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC=6![]() ,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4),(1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com