
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
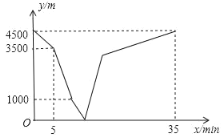
【答案】1500.
【解析】
分析图象:点A表示出发前两人相距4500米,即家和图书馆相距4500米;线段AB表示小雪已跑步出发,两人相距距离逐渐减小,到5分钟时相距3500米,即小雪5分钟走了1000米,可求小雪跑步的速度;线段BC表示小松5分钟后开始出发;点C表示两人相距1000米时,小雪改为步行,可设小雪跑步a分钟,则后面(35﹣a)分钟步行,列方程可求出a,然后用4500减1000再减去小雪走的路程可求出此时小松骑车走的路程,即求出小松的速度;点D表示两人相遇;线段DE表示两人相遇后继续往前走,点E表示小松到达家,可用路程除以小松的速度得到此时为第几分钟;线段EF表示小雪继续往图书馆走;点F表示35分钟时小雪到达图书馆.
由图象可得:家和图书馆相距4500米,小雪的跑步速度为:(4500﹣3500)÷5=200(米/分钟),
∴小雪步行的速度为:200×![]() =100(米/分钟),
=100(米/分钟),
设小雪在第a分钟时改为步行,列方程得:
200a+100(35﹣a)=4500
解得:a=10
∴小松骑车速度为:(4500﹣200×10﹣1000)÷(10﹣5)=300(米/分钟)
∴小松到家时的时间为第:4500÷300+5=20(分钟)
此时小雪离图书馆还有15分钟路程,100×15=1500(米)
故答案为1500.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
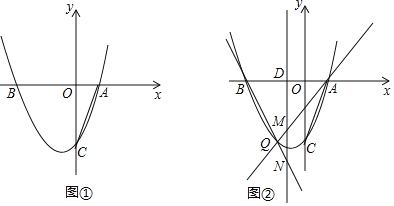
【题目】如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)如图①,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
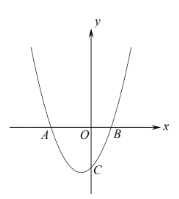
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程![]()
(1)求证:m取任何值时,方程总有实根.
(2)若二次函数![]() 的图像关于y轴对称.
的图像关于y轴对称.
a、求二次函数![]() 的解析式
的解析式
b、已知一次函数![]() ,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值
,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值![]() 均成立.
均成立.
(3)在(2)的条件下,若二次函数![]() 的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值
的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值![]() 均成立,求二次函数
均成立,求二次函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,根据习俗每家每户都会在门口挂灯笼和对联,某商店看准了商机,购进了一批红灯笼和对联进行销售,已知每幅对联的进价比每个红灯笼的进价少10元,且用480元购进对联的幅数是用同样金额购进红灯笼个数的6倍.
(1)求每幅对联和每个红灯笼的进价分别是多少?
(2)由于销售火爆,第一批销售完了以后,该商店用相同的价格再购进300幅对联和200个红灯笼,已知对联售价为6元一幅,红灯笼售价为24元一个,销售一段时间后,对联卖出了总数的![]() ,红灯笼售出了总数的
,红灯笼售出了总数的![]() ,为了清仓,该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售,并很快全部售出,求商店最低打几折可以使得这批货的总利润率不低于90%?
,为了清仓,该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售,并很快全部售出,求商店最低打几折可以使得这批货的总利润率不低于90%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),交
点的左侧),交![]() 轴于点
轴于点![]() .已知
.已知![]() .
.
(1)求抛物线的解析式;
(2)已知直线![]() ,若直线与抛物线有且只有一个交点
,若直线与抛物线有且只有一个交点![]() 求
求![]() 的面积;
的面积;
(3)在(2)的条件下,抛物线上是否存在点![]() 使
使![]() 若存在,请直接写出点
若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着近几年城市建设的快速发展.某市对花木的需求量逐年提高,某园林专业户计划投资15万元种植花卉和树木.根据市场调查与预测,种植树木的利润y1(万元)与投资量x(万元)成正比例关系,如图①所示;种植花卉的利润y2(万元)与投资量x(万元)的函数关系如图②所示(其中OA是抛物线的一部分,A为抛物线的顶点;AB//x轴)。
(1)求出y1和y2关于投资量x的函数关系式
(2)求此专业户种植花卉和树木获取的总利润W(万元)关于投入种植花卉的资金t(万元)之间的函数关系式:
(3)此专业户投入种植花卉的资金为多少万元时,才能使获取的利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买![]() 、
、![]() 两种型号的机器人搬运材料,已知
两种型号的机器人搬运材料,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运
型机器人每小时多搬运![]() 材料,且
材料,且![]() 型机器人搬运
型机器人搬运![]() 的材料所用的时间与
的材料所用的时间与![]() 型机器人搬运
型机器人搬运![]() 材料所用的时间相同.
材料所用的时间相同.
(1)求![]() 、
、![]() 两种型号的机器人每小时分别搬运多少材料?
两种型号的机器人每小时分别搬运多少材料?
(2)该公司计划采购![]() 、
、![]() 两种型号的机器人共
两种型号的机器人共![]() 台,要求每小时搬运的材料不得少于
台,要求每小时搬运的材料不得少于![]() ,则至少购进
,则至少购进![]() 型机器人多少台?
型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com