
【题目】已知如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),交
点的左侧),交![]() 轴于点
轴于点![]() .已知
.已知![]() .
.
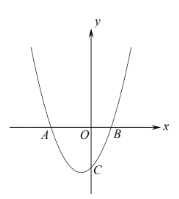
(1)求抛物线的解析式;
(2)已知直线![]() ,若直线与抛物线有且只有一个交点
,若直线与抛物线有且只有一个交点![]() 求
求![]() 的面积;
的面积;
(3)在(2)的条件下,抛物线上是否存在点![]() 使
使![]() 若存在,请直接写出点
若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)先求出点![]() 的坐标,进而求出点
的坐标,进而求出点![]() ,
,![]() 坐标,最后用待定系数法即可得出结论;
坐标,最后用待定系数法即可得出结论;
(2)联立直线![]() 与抛物线的解析式得出一元二次方程,判别式为0,求出点
与抛物线的解析式得出一元二次方程,判别式为0,求出点![]() 坐标,即可得出结论;
坐标,即可得出结论;
(3)Ⅰ、当点![]() 在
在![]() 轴上方时,先构造出
轴上方时,先构造出![]() ,进而求出点
,进而求出点![]() 的坐标,再联立直线
的坐标,再联立直线![]() 与抛物线的解析式,解方程组即可得出点
与抛物线的解析式,解方程组即可得出点![]() 坐标,
坐标,
Ⅱ、当点![]() 在
在![]() 轴下方时,判断出点
轴下方时,判断出点![]() 和点
和点![]() 关于
关于![]() 轴对称,进而联立直线
轴对称,进而联立直线![]() 与抛物线的解析式,解方程组即可得出结论.
与抛物线的解析式,解方程组即可得出结论.
解:(1)对于抛物线![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 在抛物线
在抛物线![]() 上,
上,
![]()
![]() ,
,
![]()
![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)由(1)知,抛物线的解析式为![]() ①,
①,
![]() 直线
直线![]() ②与抛物线有且只有一个交点
②与抛物线有且只有一个交点![]() ,
,
联立①②得,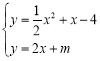 ,
,
![]()
![]() ,
,
![]() △
△![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]()
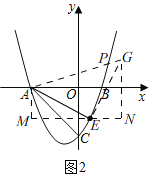
如图1,记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,则
,则![]() ,
,
![]() ;
;
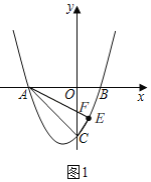
(3)由(2)知,![]() ,
,
Ⅰ、当点![]() 在
在![]() 轴上方时,如图2,
轴上方时,如图2,
将线段![]() 以点
以点![]() 为旋转中心顺时针旋转
为旋转中心顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 与抛物线的交点,
与抛物线的交点,
过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
由旋转知,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ③,
③,
![]() 抛物线的解析式为
抛物线的解析式为![]() ④,
④,
联立③④解得,![]() 或
或 ,
,
![]() ,
,![]() ,
,
Ⅱ、由Ⅰ知,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]() 点
点![]() 是直线
是直线![]() 与抛物线的交点,
与抛物线的交点,
![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ⑤,
⑤,
联立④⑤,解得,![]() 或
或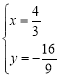 ,
,
![]() ,
,![]() ,即满足条件的点
,即满足条件的点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
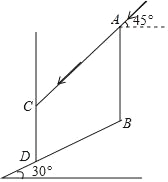
【题目】如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A,B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.
(1)求这两种马路清扫车的单价;
(2)恰逢该厂举行30周年庆,决定对这两种马路清扫车开展促销活动,具体方案如下:购买A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售.设购买x辆A种马路清扫车需要y1元,购买x(x>0)个B型马路清扫车需要y2元,分别求出y1,y2关于x的函数关系式;
(3)若该公司承包的道路清扫面积为118000m2,每辆A型马路清扫车每天清扫5000m2,每辆B型马路清扫车每天清扫6000m2,公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
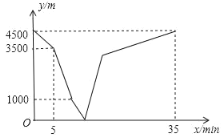
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
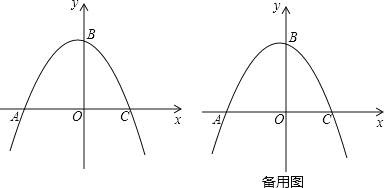
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八。问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文,如果乙得到甲所有钱的![]() ,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过A(﹣2,0),B(0,2),C(![]() ,0)三点,一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交y轴于点Q.设点P的运动时间为t秒.
,0)三点,一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交y轴于点Q.设点P的运动时间为t秒.
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P的运动,抛物线上是否存在一点M,使△MPQ为等边三角形?若存在,请直接写t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com