
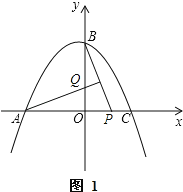
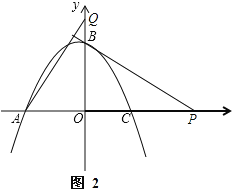
����Ŀ����֪�����߾���A(��2��0)��B(0��2)��C(![]() ��0)���㣬һ����P��ԭ�������1����λ/����ٶ���x���������˶�������BP������A��ֱ��BP�Ĵ��߽�y���ڵ�Q�����P���˶�ʱ��Ϊt�룮
��0)���㣬һ����P��ԭ�������1����λ/����ٶ���x���������˶�������BP������A��ֱ��BP�Ĵ��߽�y���ڵ�Q�����P���˶�ʱ��Ϊt�룮
(1)�������ߵĽ���ʽ��
(2)��BQ=![]() APʱ����t��ֵ��
APʱ����t��ֵ��
(3)���ŵ�P���˶������������Ƿ����һ��M��ʹ��MPQΪ�ȱ������Σ������ڣ���ֱ��дt��ֵ����Ӧ��M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y=��![]() x2��
x2��![]() x+2 ��(2) t=
x+2 ��(2) t=![]() ��6ʱ��BQ=
��6ʱ��BQ=![]() AP��(3) ��t=
AP��(3) ��t=![]() ��1ʱ���������ϴ��ڵ�M(1��1)����t=3+3
��1ʱ���������ϴ��ڵ�M(1��1)����t=3+3![]() ʱ���������ϴ��ڵ�M(��3����3)��
ʱ���������ϴ��ڵ�M(��3����3)��
��������
��1�����ô���ϵ��������3������������ã�
��2������2���������Q�ڵ�B���·����Ϸ�������BQ=![]() AP�����t��ֵ��
AP�����t��ֵ��
��3����֤��AOQ�ա�BOP���õ���OPQΪ����ֱ�������Σ���M�����PQ�Ĵ�ֱƽ�����ϣ���M��y=x�ϣ�������M���������ϵķ��̣����M��2����������������MPQΪ�ȱ������εļ������ʷ�����⼴�ɣ�
�⣺(1)�������ߵĽ���ʽΪy=ax2+bx+c��
�������߾���A(��2��0)��B(0��2)��C(![]() ��0)���㣬
��0)���㣬
�� ��
��
��� ��
��
��y=![]() x2
x2![]() x+2��
x+2��
(2)��AQ��PB��BO��AP��
���AOQ=��BOP=90������PAQ=��PBO��
��AO=BO=2��
���AOQ�ա�BOP��
��OQ=OP=t��
����ͼ1����t��2ʱ����Q�ڵ�B�·�����ʱBQ=2��t��AP=2+t��
��BQ=![]() AP��
AP��
��2��t=![]() (2+t)��
(2+t)��
��t=![]() ��
��
����ͼ2����t��2ʱ����Q�ڵ�B�Ϸ�����ʱBQ=t��2��AP=2+t��
��BQ=![]() AP��
AP��
��t��2=![]() (2+t)��
(2+t)��
��t=6��
����������t=![]() ��6ʱ��BQ=
��6ʱ��BQ=![]() AP��
AP��
(3)��t=![]() ��1ʱ���������ϴ��ڵ�M(1��1)����t=3+3
��1ʱ���������ϴ��ڵ�M(1��1)����t=3+3![]() ʱ���������ϴ��ڵ�M(��3����3)��
ʱ���������ϴ��ڵ�M(��3����3)��
�������£�
��AQ��BP��
���QAO+��BPO=90����
�ߡ�QAO+��AQO=90����
���AQO=��BPO��
�ڡ�AOQ�͡�BOP�У�
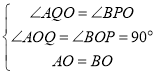 ��
��
���AOQ�ա�BOP��
��OP=OQ��
���OPQΪ����ֱ�������Σ�
�ߡ�MPQΪ�ȱ������Σ���M�����PQ�Ĵ�ֱƽ�����ϣ�
��ֱ��y=x��ֱƽ��PQ��
��M��y=x�ϣ���M(x��y)��
��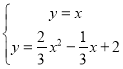 ��
��
���![]() ��
��![]() ��
��
��M�����Ϊ(1��1)��(��3����3)��
����ͼ3����M������Ϊ(1��1)ʱ����MD��x����D��
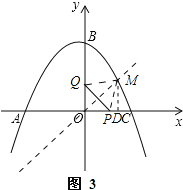
����PD=|1��t|��MP2=1+|1��t|2=t2��2t+2��PQ2=2t2��
�ߡ�MPQΪ�ȱ������Σ�
��MP=PQ��
��t2+2t��2=0��
��t=��1+![]() ��t=��1��
��t=��1��![]() (��ֵ��ȥ)��
(��ֵ��ȥ)��
����ͼ4����M������Ϊ(��3����3)ʱ����ME��x����E��
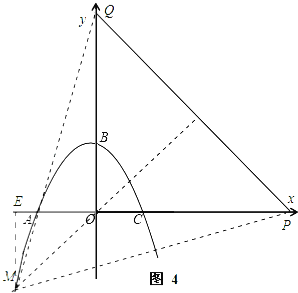
����PE=3+t��ME=3��
��MP2=32+(3+t)2=t2+6t+18��PQ2=2t2��
�ߡ�MPQΪ�ȱ������Σ�
��MP=PQ��
��t2��6t��18=0��
��t=3+3![]() ��t=3��3
��t=3��3![]() (��ֵ��ȥ)��
(��ֵ��ȥ)��
������������t=��1+![]() ʱ���������ϴ��ڵ�M(1��1)����t=3+3
ʱ���������ϴ��ڵ�M(1��1)����t=3+3![]() ʱ���������ϴ��ڵ�M(��3����3)��ʹ�á�MPQΪ�ȱ������Σ�
ʱ���������ϴ��ڵ�M(��3����3)��ʹ�á�MPQΪ�ȱ������Σ�


 ��������ѧ����ϵ�д�
��������ѧ����ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
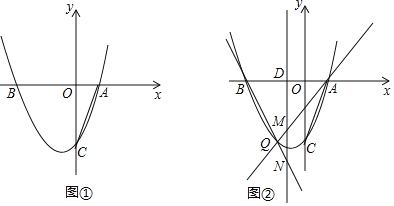
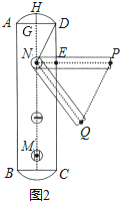
����Ŀ����ͼ��������y��x2+bx+c��x����A��B���㣬���е�A����Ϊ��1��0������y�ύ�ڵ�C��0����3����
��1���������ߵĺ�������ʽ��
��2����ͼ�٣�����AC����P���������ϣ��������PAB��2��ACO�����P�����ꣻ
��3����ͼ�ڣ���QΪx���·�������������һ�㣬��D�������߶Գ�����x��Ľ��㣬ֱ��AQ��BQ�ֱ������ߵĶԳ����ڵ�M��N������DM+DN�Ƿ�Ϊ��ֵ������ǣ�����������ֵ��������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��������![]() ��
��![]() ����
����![]() ����(
����(![]() ����
����![]() ������)����
������)����![]() ���ڵ�
���ڵ�![]() .��֪
.��֪![]() ��
��
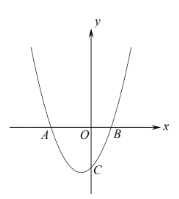
��1���������ߵĽ���ʽ��
��2����ֱ֪��![]() ����ֱ��������������ֻ��һ������
����ֱ��������������ֻ��һ������![]() ��
��![]() �������
�������
��3���ڣ�2���������£����������Ƿ���ڵ�![]() ʹ
ʹ![]() �����ڣ���ֱ��д����
�����ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ž�������н���Ŀ��ٷ�չ.ij�жԻ�ľ��������������ߣ�ij��רҵ���ƻ�Ͷ��15��Ԫ��ֲ���ܺ���ľ.�����г�������Ԥ�⣬��ֲ��ľ������y1(��Ԫ)��Ͷ����x(��Ԫ)����������ϵ����ͼ����ʾ����ֲ���ܵ�����y2(��Ԫ)��Ͷ����x(��Ԫ)�ĺ�����ϵ��ͼ����ʾ������OA�������ߵ�һ���֣�AΪ�����ߵĶ��㣻AB//x�ᣩ��
(1)���y1��y2����Ͷ����x�ĺ�����ϵʽ
(2)���רҵ����ֲ���ܺ���ľ��ȡ��������W(��Ԫ)����Ͷ����ֲ���ܵ��ʽ�t(��Ԫ)֮��ĺ�����ϵʽ:
(3)��רҵ��Ͷ����ֲ���ܵ��ʽ�Ϊ������Ԫʱ������ʹ��ȡ�����������������Ƕ���?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ�������˴ʻ������Ϊ�˽���ڶ�����ʻ�����⣬ij��ȤС�������һ��������·�˼����ĵ�����ѡȡ�ĸ��ȴ�A����Ӳ����������B��������Ŷ����C����˫��666����D�����ܾ�ʱ�����ڽֵ��϶�������Ⱥ�����˳������飬Ҫ�����ÿλֻ�ܹ�ѡһ������Ϥ���ȴʣ����ݵ���������С����������µ�������������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ������������⣺
(1)���ε����У�һ���������� ����·�ˣ�
(2)��ȫ����ͳ��ͼ��
(3)����ͼ�е�b=�� ����
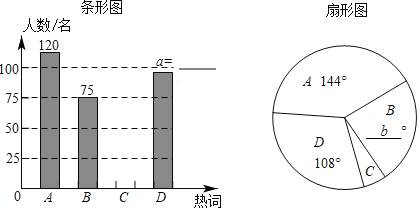
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ף� ����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������ա���ɳ���ա��������ա���������(���·ֱ���A��B��C��D��ʾ)�����ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ(�в�����)�� �����������Ϣ�ش�
(1)���βμӳ�������ľ����ж����ˣ�
(2)��������������ͼ����������
(3)����������8000�ˣ�����ư���D�յ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ҵ��ſ���װ��һ�ѷ�����������ͼ1������ƽ��ṹͼ��ͼ2��ʾ���������Կ����������Ȼ�![]() ��
��![]() �;���
�;���![]() ��ɵģ�
��ɵģ�![]() ��Բ���ǵ�����ť��
��Բ���ǵ�����ť��![]() ����֪
����֪![]() �Ĺ��θ�
�Ĺ��θ�![]() ��
��![]() ��
��![]() ��������
��������![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת��
˳ʱ����ת��![]() λ��ʱ����������ʱֱ��
λ��ʱ����������ʱֱ��![]() ��
��![]() ���ڵ�Բ���У���
���ڵ�Բ���У���![]() ��
��![]() ��
��
��1����![]() ����Բ�İ뾶��
����Բ�İ뾶��
��2�����߶�![]() �ij��ȣ���
�ij��ȣ���![]() �������ȷ��
�������ȷ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����![]() ��
��![]() �����ͺŵĻ����˰��˲��ϣ���֪
�����ͺŵĻ����˰��˲��ϣ���֪![]() �ͻ����˱�
�ͻ����˱�![]() �ͻ�����ÿСʱ�����
�ͻ�����ÿСʱ�����![]() ���ϣ���
���ϣ���![]() �ͻ����˰���
�ͻ����˰���![]() �IJ������õ�ʱ����
�IJ������õ�ʱ����![]() �ͻ����˰���
�ͻ����˰���![]() �������õ�ʱ����ͬ��
�������õ�ʱ����ͬ��
��1����![]() ��
��![]() �����ͺŵĻ�����ÿСʱ�ֱ���˶��ٲ��ϣ�
�����ͺŵĻ�����ÿСʱ�ֱ���˶��ٲ��ϣ�
��2���ù�˾�ƻ��ɹ�![]() ��
��![]() �����ͺŵĻ����˹�
�����ͺŵĻ����˹�![]() ̨��Ҫ��ÿСʱ���˵IJ��ϲ�������
̨��Ҫ��ÿСʱ���˵IJ��ϲ�������![]() �������ٹ���
�������ٹ���![]() �ͻ����˶���̨��
�ͻ����˶���̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ѧ���ԡ�Ԥ������״������֪ʶ�����������ѧУ��֯��һ������֪ʶ��ѵ����ѵ��������в��ԣ���ȫУ2000��ѧ���У��ֱ��ȡ��������Ů����15�ݳɼ������������������£��벹��������
���ռ����ݣ�
15���������Գɼ�ͳ�����£�������100�֣�78��90��99��93��92��95��94��100��90��85��86��95��75��88��90
15��Ů�����Գɼ�ͳ�����£�������100�֣�77��82��83��86��90��90��92��91��93��92��92��92��92��98��100
���������������ݣ�
70.5��75.5 | 75.5��80.5 | 80.5��85.5 | 85.5��90.5 | 90.5��95.5 | 95.5��100.5 | |
���� | 1 | 1 | 1 | 5 | 5 | 2 |
�� | 0 | 1 | 2 | 3 | 7 | 2 |
���������ݣ�
��1�������������ݵ�ƽ��������������λ�����������±���ʾ��
�Ա� | ƽ���� | ���� | ��λ�� | ���� |
���� | 90 | 90 | 90 | 44.9 |
�� | 90 |
|
| 32.8 |
�ڱ��У�![]() ________��
________��![]() ________��
________��
��2�����涨�÷���80�����ϣ�����80�֣�Ϊ�ϸ������ȫУѧ���С�Ԥ������״������֪ʶ���Ժϸ��ѧ���ж����ˣ�
��3��ͨ�����ݷ����õ��Ľ��ۣ�����Ϊ������Ů����˭�ijɼ��ȽϺã���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com