
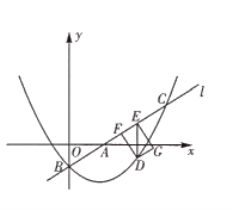
����Ŀ�����Ž�������н���Ŀ��ٷ�չ.ij�жԻ�ľ��������������ߣ�ij��רҵ���ƻ�Ͷ��15��Ԫ��ֲ���ܺ���ľ.�����г�������Ԥ�⣬��ֲ��ľ������y1(��Ԫ)��Ͷ����x(��Ԫ)����������ϵ����ͼ����ʾ����ֲ���ܵ�����y2(��Ԫ)��Ͷ����x(��Ԫ)�ĺ�����ϵ��ͼ����ʾ������OA�������ߵ�һ���֣�AΪ�����ߵĶ��㣻AB//x�ᣩ��
(1)���y1��y2����Ͷ����x�ĺ�����ϵʽ
(2)���רҵ����ֲ���ܺ���ľ��ȡ��������W(��Ԫ)����Ͷ����ֲ���ܵ��ʽ�t(��Ԫ)֮��ĺ�����ϵʽ:
(3)��רҵ��Ͷ����ֲ���ܵ��ʽ�Ϊ������Ԫʱ������ʹ��ȡ�����������������Ƕ���?

���𰸡���1��y1=2x��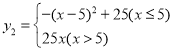 ����2��
����2��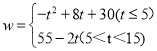 ����3����t=4ʱ��Wȡ�����ֵΪ46��.
����3����t=4ʱ��Wȡ�����ֵΪ46��.
��������
(1)��y2(��Ԫ)��Ͷ����x(��Ԫ)�ĺ�����ϵͼ��֪����0<x��5ʱy2��x�Ĺ�ϵʽͼ��Ϊ���κ���ͼ���һ���֣���x>5ʱ��y2=25����Ӧ�����������
(2)����(1)�������ϵʽ��y1=2x����Ͷ��15��Ԫ���г�����w��t�ĺ�����ϵʽ��
(3)��(2)��w��t�Ĺ�ϵʽ���w�����ֵ���ɣ�
�⣺(1)��y1=kx����ͼ����ʾ������y1=kx��ͼ���(1��2)��
����2=k1��k=2��������y1����Ͷ����x�ĺ�����ϵʽ��y1=2x��
�ɺ���ͼ���֪����x��5ʱ��y2��x�Ĺ�ϵʽͼ��Ϊ�����ߵ�һ���֣�
��������ߵĽ���ʽΪ��y2=a(x-5)2+25��
��(0��0)�������ʽ�ã�0=25a+25(x��5)�����a=-1��
�ʺ�������ʽΪy2=-(x-5)2+25(x��5)��
��x��5ʱ��y2=25(x��5����
��y2��x�Ĺ�ϵʽΪ ��
��
(2)��ΪͶ����ֲ����t��Ԫ����Ͷ����ֲ��ľ��15-t����Ԫ��
��t��5ʱ��y1=2(15-t)��y2=-(t-5)2+25��
��W=-(t-5)2+25+2(15-t)=-t2+8t+30��
��5��t��15ʱ��y1=2(15-t)��y2=25��
��W=55-2t��������W(��Ԫ)����Ͷ����ֲ���ܵ��ʽ�t(��Ԫ)֮��ĺ�����ϵʽ��
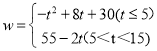
(3)��t��5ʱW=-t2+8t+30�����ݶ��κ��������ʣ���![]() ��Ԫʱ��Wȡ�����ֵ��W���ֵ=-42+8��4+30=-16+32+30=46��
��Ԫʱ��Wȡ�����ֵ��W���ֵ=-42+8��4+30=-16+32+30=46��
��5��t��15����-2��0��w��t���������С������t=5ʱ��w���ֵΪ45����45��46��
����t=4ʱ��Wȡ�����ֵΪ46��.
�ʴ�Ϊ��(1)y1=2x�� ��(2)
��(2)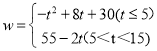 ����3����t=4ʱ��Wȡ�����ֵΪ46��.
����3����t=4ʱ��Wȡ�����ֵΪ46��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ס��ҡ�����λͬѧ���5����ѧ�ɼ��������ڰ༶��Ӧƽ���ֵ�����ͳ��ͼ���������жϴ������( ).

A. ����ѧ�ɼ����ڰ༶ƽ���֣��ҳɼ��Ƚ��ȶ�
B. �ҵ���ѧ�ɼ��ڰ༶ƽ���ָ����������ұȱ���
C. ������ѧ�ɼ����ڰ༶ƽ���֣����ɼ�������
D. �ͼס��ҡ��������˶��ԣ��ҵ���ѧ�ɼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
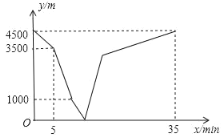
����Ŀ��Сѩ��С�ɷֱ�ӼҺ�ͼ��ݳ�������ͬһ����ֱ����·������У�Сѩ��ʼ�ܲ�����;��ij�ظ�Ϊ���У��Ҳ��е��ٶ�Ϊ�ܲ��ٶȵ�һ�룬Сѩ�ȳ���5���Ӻ�С�ɲ������г����ٻؼң�Сѩ����ͼ���ǡ������35���ӣ�����֮��ľ���y��m����Сѩ�뿪�����ص�ʱ��x��min��֮��ĺ���ͼ����ͼ��ʾ����С�ɸյ���ʱ��Сѩ��ͼ��ݵľ���Ϊ____�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD �У���E��O��F�ֱ��DZ�AB��AC��AD���е㣬����CE��CF��OE��OF��
��1����֤����BCE�ա�DCF��
��2����AB��BC����ʲô����ʱ���ı���AEOF�����Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㾭�����й��Ŵ���Ҫ����ѧ���������м���:�����мס��Ҷ��ˣ���Ǯ����֪��.�����а룬������ʮ�ˣ��ҵü�̫�룬������ʮ�ˡ��ʼס��Ҷ���ԭ��Ǯ������?������:���ף������˸�������Ǯ������õ�������Ǯ��һ�룬��ô����Ǯ48�ģ�����ҵõ�������Ǯ��![]() ����ô��Ҳ����Ǯ48�ģ��ʼס��Ҷ���ԭ�����ж���Ǯ?��
����ô��Ҳ����Ǯ48�ģ��ʼס��Ҷ���ԭ�����ж���Ǯ?��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
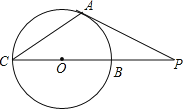
����Ŀ����ͼ��PA�С�O�ڵ�A��PC����O�����O����B��C���㣬��PA=6cm��PB=2![]() cm�����PAC�������_____cm2��
cm�����PAC�������_____cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
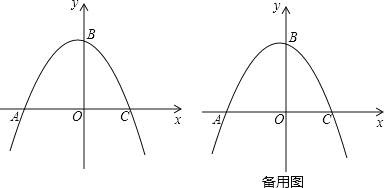
����Ŀ����֪�����߾���A(��2��0)��B(0��2)��C(![]() ��0)���㣬һ����P��ԭ�������1����λ/����ٶ���x���������˶�������BP������A��ֱ��BP�Ĵ��߽�y���ڵ�Q�����P���˶�ʱ��Ϊt�룮
��0)���㣬һ����P��ԭ�������1����λ/����ٶ���x���������˶�������BP������A��ֱ��BP�Ĵ��߽�y���ڵ�Q�����P���˶�ʱ��Ϊt�룮
(1)�������ߵĽ���ʽ��
(2)��BQ=![]() APʱ����t��ֵ��
APʱ����t��ֵ��
(3)���ŵ�P���˶������������Ƿ����һ��M��ʹ��MPQΪ�ȱ������Σ������ڣ���ֱ��дt��ֵ����Ӧ��M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2��bx��c��ͼ�����(��1,0)�͵�(3,0)��������˵������bc��0����a��b��c��0����2a��b��0����4ac��b2�����д������(����)
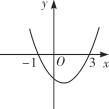
A.�ڢ�B.�٢ۢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��
��![]() ���
���![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() �͵�
�͵�![]() ������
������![]() ������
������![]() ��ֱ��
��ֱ��![]() ����һ������Ϊ
����һ������Ϊ![]() ��
��
![]() ��
��![]() ��ֵ�������ߵĽ���ʽ
��ֵ�������ߵĽ���ʽ
![]() ��
��![]() ���������ϣ�
���������ϣ�![]() �ύֱ��
�ύֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϣ����ı���
�ϣ����ı���![]() Ϊ���Σ����
Ϊ���Σ����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ��
��![]() ��
��![]() �ĺ�����ϵʽ�Լ�
�ĺ�����ϵʽ�Լ�![]() �����ֵ
�����ֵ
![]() ��
��![]() ��ƽ����ij��
��ƽ����ij��![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����
����![]() �ֱ���
�ֱ���![]() ���Ӧ)����
���Ӧ)����![]() ����������ǡ�������������ϣ���ֱ��д����
����������ǡ�������������ϣ���ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com