
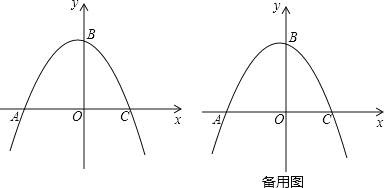
【题目】如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数表达式;
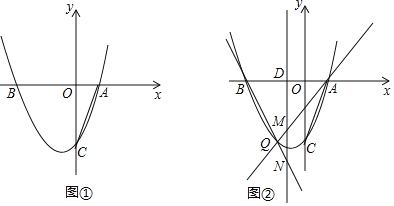
(2)如图①,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)抛物线的函数表达式为y=x2+2x﹣3;(2)点P的坐标为![]() ,
,![]() 或
或![]() ,
,![]() ;(3)为定值8.
;(3)为定值8.
【解析】
(1)把点![]() 、
、![]() 坐标代入抛物线解析式即求得
坐标代入抛物线解析式即求得![]() 、
、![]() 的值.
的值.
(2)点![]() 可以在
可以在![]() 轴上方或下方,需分类讨论.①若点
轴上方或下方,需分类讨论.①若点![]() 在
在![]() 轴下方,延长
轴下方,延长![]() 到
到![]() ,使
,使![]() 构造等腰
构造等腰![]() ,作
,作![]() 中点
中点![]() ,即有
,即有![]() ,利用
,利用![]() 的三角函数值,求
的三角函数值,求![]() 、
、![]() 的长,进而求得
的长,进而求得![]() 的坐标,求得直线
的坐标,求得直线![]() 的解析式后与抛物线解析式联立,即求出点
的解析式后与抛物线解析式联立,即求出点![]() 坐标.②若点
坐标.②若点![]() 在
在![]() 轴上方,根据对称性,
轴上方,根据对称性,![]() 一定经过点
一定经过点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,求得直线
,求得直线![]() 的解析式后与抛物线解析式联立,即求出点
的解析式后与抛物线解析式联立,即求出点![]() 坐标.
坐标.
(3)设点![]() 横坐标为
横坐标为![]() ,用
,用![]() 表示直线
表示直线![]() 、
、![]() 的解析式,把
的解析式,把![]() 分别代入即求得点
分别代入即求得点![]() 、
、![]() 的纵坐标,再求
的纵坐标,再求![]() 、
、![]() 的长,即得到
的长,即得到![]() 为定值.
为定值.
解:(1)∵抛物线y=x2+bx+c经过点A(1,0),C(0,﹣3)
![]()
![]() 解得:
解得:![]()
∴抛物线的函数表达式为y=x2+2x﹣3
(2)①若点P在x轴下方,如图1,
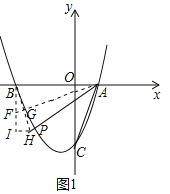
延长AP到H,使AH=AB,过点B作BI⊥x轴,连接BH,作BH中点G,连接并延长AG交BI于点F,过点H作HI⊥BI于点I
∵当x2+2x﹣3=0,解得:x1=﹣3,x2=1
∴B(﹣3,)
∵A(1,0),C(0,﹣3)
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 中,
中,![]() ,
,![]()
∵AB=AH,G为BH中点
∴AG⊥BH,BG=GH
∴∠BAG=∠HAG,即∠PAB=2∠BAG
∵∠PAB=2∠ACO
∴∠BAG=∠ACO
![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,即
,即![]() ,
,![]()
设直线![]() 解析式为
解析式为![]()
![]()
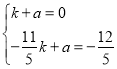 解得:
解得: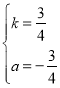
![]() 直线
直线![]()
![]()
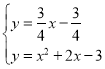 解得:
解得: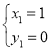 (即点
(即点![]() ,
,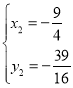
![]() ,
,![]() ;
;
②若点![]() 在
在![]() 轴上方,如图2,
轴上方,如图2,
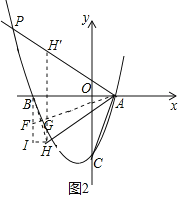
在![]() 上截取
上截取![]() ,则
,则![]() 与
与![]() 关于
关于![]() 轴对称
轴对称
![]() ,
,![]()
设直线![]() 解析式为
解析式为![]()
![]()
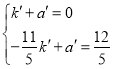 解得:
解得:
![]() 直线
直线![]()
![]()
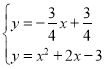 解得:
解得: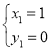 (即点
(即点![]() ,
,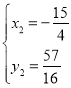
![]() ,
,![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.
(3)![]() 为定值,
为定值,
![]() 抛物线
抛物线![]() 的对称轴为:直线
的对称轴为:直线![]()
![]() ,
,![]()
设![]() ,
,![]()
设直线![]() 解析式为
解析式为![]()
![]()
![]() 解得:
解得: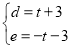
![]() 直线
直线![]()
当![]() 时,
时,![]()
![]()
设直线![]() 解析式为
解析式为![]()
![]()
![]() 解得:
解得:![]()
![]() 直线
直线![]()
当![]() 时,
时,![]()
![]()
![]() ,为定值.
,为定值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号).
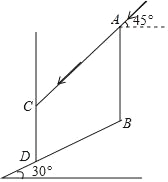
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;
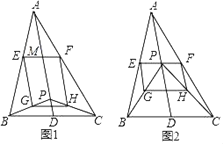
(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;
(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A,B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.
(1)求这两种马路清扫车的单价;
(2)恰逢该厂举行30周年庆,决定对这两种马路清扫车开展促销活动,具体方案如下:购买A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售.设购买x辆A种马路清扫车需要y1元,购买x(x>0)个B型马路清扫车需要y2元,分别求出y1,y2关于x的函数关系式;
(3)若该公司承包的道路清扫面积为118000m2,每辆A型马路清扫车每天清扫5000m2,每辆B型马路清扫车每天清扫6000m2,公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
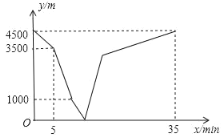
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过A(﹣2,0),B(0,2),C(![]() ,0)三点,一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交y轴于点Q.设点P的运动时间为t秒.
,0)三点,一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交y轴于点Q.设点P的运动时间为t秒.
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P的运动,抛物线上是否存在一点M,使△MPQ为等边三角形?若存在,请直接写t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com