
ЁОЬтФПЁПШчЙћЫФБпаЮгавЛзщЖдБпЦНааЃЌЧвСэвЛзщЖдБпВЛЦНааЃЌФЧУДГЦетбљЕФЫФБпаЮЮЊЬнаЮЃЌШєЬнаЮжагавЛИіНЧЪЧжБНЧЃЌдђГЦЦфЮЊжБНЧЬнаЮЃЎЯТУцЫФИіНсТлжаЃК
ЂйДцдкЮоЪ§ИіжБНЧЬнаЮЃЌЦфЫФИіЖЅЕуЗжБ№дкЭЌвЛИіе§ЗНаЮЕФЫФЬѕБпЩЯЃЛ
ЂкДцдкЮоЪ§ИіжБНЧЬнаЮЃЌЦфЫФИіЖЅЕудкЭЌвЛЬѕХзЮяЯпЩЯЃЛ
ЂлДцдкЮоЪ§ИіжБНЧЬнаЮЃЌЦфЫФИіЖЅЕудкЭЌвЛИіЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЛ
ЂмжСЩйДцдквЛИіжБНЧЬнаЮЃЌЦфЫФИіЖЅЕудкЭЌвЛИідВЩЯЃЎ
Ыљгае§ШЗНсТлЕФађКХЪЧ_____ЃЎ
ЁОД№АИЁПЂйЂкЂл
ЁОНтЮіЁП
ИљОнжБНЧЬнаЮЕФаджЪЃЌЛГіЭМаЮРћгУЭМЯѓЗЈвЛвЛХаЖЯМДПЩЃЎ
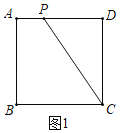
ЂйШчЭМ1жаЃЌЕуPЪЧе§ЗНаЮABCDЕФБпADЩЯЕФШЮвтвЛЕуЃЌдђЫФБпаЮABCPЪЧжБНЧЬнаЮЃЌетбљЕФжБНЧЬнаЮгаЮоЪ§ИіЃЌЙЪЂйе§ШЗЃЎ
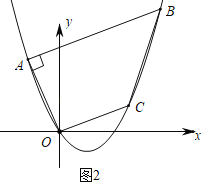
ЂкШчЭМ2жаЃЌЫФБпаЮABCOЪЧжБНЧЬнаЮЃЌетбљЕФжБНЧЬнаЮгаЮоЪ§ИіЃЌЙЪЂке§ШЗЃЎ
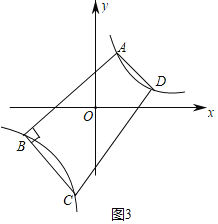
ЂлШчЭМ3жаЃЌЫФБпаЮABCDЪЧжБНЧЬнаЮЃЌетбљЕФжБНЧЬнаЮгаЮоЪ§ИіЃЌЙЪЂле§ШЗЃЎ
ЂмжБНЧЬнаЮЕФЫФИіЖЅЕуЃЌВЛПЩФмдкЭЌвЛИідВЩЯЃЌЙЪЂмДэЮѓЃЌ
ЙЪД№АИЮЊЃКЂйЂкЂлЃЎ


 аТПЮБъНзЬндФЖСбЕСЗЯЕСаД№АИ
аТПЮБъНзЬндФЖСбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020ФъаТЙкЗЮбзвпЧщЗЂЩњвдРДЃЌЮвЪаЙуДѓдкжАЕГдБЛ§МЋВЮгыЩчЧјЗРвпЙЄзїЃЌжњСІЩчЧјМсОіДђгЎвпЧщЗРПизшЛїеНЃЎЦфжаЃЌ![]() ЩчЧјга500УћдкжАЕГдБЃЌЮЊСЫНтБОЩчЧј2дТ-3дТЦкМфдкжАЕГдБВЮМггІМБжДЧкЕФЧщПіЃЌ
ЩчЧјга500УћдкжАЕГдБЃЌЮЊСЫНтБОЩчЧј2дТ-3дТЦкМфдкжАЕГдБВЮМггІМБжДЧкЕФЧщПіЃЌ![]() ЩчЧјеыЖджДЧкЕФДЮЪ§ЫцЛњГщШЁ50УћдкжАЕГдБНјааЕїВщЃЌВЂЖдЪ§ОнНјааСЫећРэЁЂУшЪіКЭЗжЮіЃЌЯТУцИјГіСЫВПЗжаХЯЂЃЎ
ЩчЧјеыЖджДЧкЕФДЮЪ§ЫцЛњГщШЁ50УћдкжАЕГдБНјааЕїВщЃЌВЂЖдЪ§ОнНјааСЫећРэЁЂУшЪіКЭЗжЮіЃЌЯТУцИјГіСЫВПЗжаХЯЂЃЎ
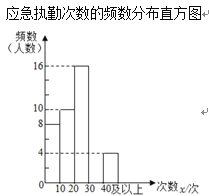
ЦфжаЃЌгІМБжДЧкДЮЪ§дк![]() етвЛзщЕФЪ§ОнЪЧЃК
етвЛзщЕФЪ§ОнЪЧЃК
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
ЧыИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
ЃЈ2ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉЫцЛњГщШЁЕФ50УћдкжАЕГдБВЮМггІМБжДЧкДЮЪ§ЕФжаЮЛЪ§ЪЧ______ЃЛ
ЃЈ4ЃЉЧыЙРМЦ2дТ-3дТЦкМф![]() ЩчЧјдкжАЕГдБВЮМггІМБжДЧкЕФДЮЪ§ВЛЕЭгк30ДЮЕФдМга______ШЫЃЎ
ЩчЧјдкжАЕГдБВЮМггІМБжДЧкЕФДЮЪ§ВЛЕЭгк30ДЮЕФдМга______ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПББОЉФГГЌЪаАДдТЖЉЙКвЛжжЫсФЬЃЌУПЬьЕФНјЛѕСПЯрЭЌЃЎИљОнЭљФъЕФЯњЪлОбщЃЌУПЬьашЧѓСПгыЕБЬьзюИпЦјЮТЃЈЕЅЮЛЃКЁцЃЉгаЙиЃЎЮЊСЫШЗЖЈНёФъСљдТЗнЕФЫсФЬЖЉЙКМЦЛЎЃЌЖдЧАШ§ФъСљдТЗнЕФзюИпЦјЮТМАИУЫсФЬашЧѓСПЪ§ОнНјааСЫећРэЁЂУшЪіКЭЗжЮіЃЌЯТУцИјГіСЫВПЗжаХЯЂЃЎ
aЃЎЫсФЬУПЬьашЧѓСПгыЕБЬьзюИпЦјЮТЙиЯЕШчБэЃК
зюИпЦјЮТtЃЈЕЅЮЛЃКЁцЃЉ | 20ЁмtЃМ25 | 25ЁмtЃМ30 | 30ЁмtЁм40 |
ЫсФЬашЧѓСПЃЈЕЅЮЛЃКЦП/ЬьЃЉ | 300 | 400 | 600 |
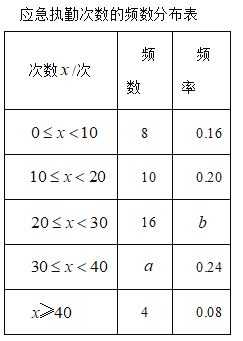
b.2017Фъ6дТзюИпЦјЮТЪ§ОнЕФЦЕЪ§ЗжВМЭГМЦБэШчБэЃЈВЛЭъећЃЉЃК
2017Фъ6дТзюИпЦјЮТЪ§ОнЕФЦЕЪ§ЗжВМБэЃК
Зжзщ | ЦЕЪ§ | ЦЕТЪ |
20ЁмtЃМ25 | 3 | |
25ЁмtЃМ30 | m | 0.20 |
30ЁмtЃМ35 | 14 | |
35ЁмtЁм40 | 0.23 | |
КЯМЦ | 30 | 1.00 |
c.2018Фъ6дТзюИпЦјЮТЪ§ОнЕФЦЕЪ§ЗжВМжБЗНЭМШчЭМЃК
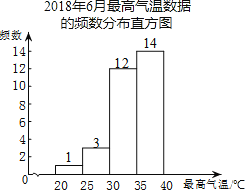
d.2019Фъ6дТзюИпЦјЮТЪ§ОнШчЯТЃЈЮДАДШеЦкЫГађЃЉЃК
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉmЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉ2019Фъ6дТзюИпЦјЮТЪ§ОнЕФжкЪ§ЮЊЁЁ ЁЁЃЌжаЮЛЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3
ЃЈ4ЃЉвбжЊИУЫсФЬНјЛѕГЩБОУПЦП4дЊЃЌЪлМлУПЦП6дЊЃЌЮДЪлГіЕФЫсФЬНЕМлДІРэЃЌвдУПЦП2дЊЕФМлИёЕБЬьШЋВПДІРэЭъЃЎ
Ђй2019Фъ6дТетжжЫсФЬУПЬьЕФНјЛѕСПЮЊ500ЦПЃЌдђДЫдТетжжЫсФЬЕФРћШѓЮЊЁЁ ЁЁдЊЃЛ
ЂкИљОнвдЩЯаХЯЂЃЌдЄЙР2020Фъ6дТетжжЫсФЬЖЉЙКЕФНјЛѕСПВЛКЯРэЕФЮЊЁЁ ЁЁЃЎ
AЃЎ550ЦП/Ьь
BЃЎ600ЦП/Ьь
CЃЎ380ЦП/Ьь
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЁЂаЁДЯВЮМгСЫ100mХмЕФ5ЦкМЏбЕЃЌУПЦкМЏбЕНсЪјЪБНјааВтЪдЃЌИљОнЫћУЧЕФМЏбЕЪБМфЁЂВтЪдГЩМЈЛцжЦГЩШчЭМСНИіЭГМЦЭМЃЎ
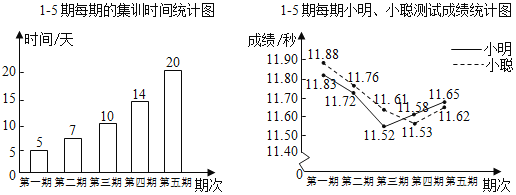
ИљОнЭМжааХЯЂЃЌгаЯТУцЫФИіЭЦЖЯЃК
Ђйет5ЦкЕФМЏбЕЙВга56ЬьЃЛ
ЂкаЁУї5ДЮВтЪдЕФЦНОљГЩМЈЪЧ11.68УыЃЛ
ЂлДгМЏбЕЪБМфПДЃЌМЏбЕЪБМфВЛЪЧдНЖрдНКУЃЌМЏбЕЪБМфЙ§ГЄЃЌПЩФмдьГЩРЭРлЃЌЕМжТГЩМЈЯТЛЌЃЛ
ЂмДгВтЪдГЩМЈПДЃЌСНШЫЕФзюКУГЩМЈЖМЪЧдкЕк4ЦкГіЯжЃЌНЈвщМЏбЕЪБМфЖЈЮЊ14ЬьЃЎ
ЫљгаКЯРэЭЦЖЯЕФађКХЪЧЃЈЁЁЁЁЃЉ
A.ЂйЂлB.ЂкЂмC.ЂкЂлD.ЂйЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕxOyжаЃЌКЏЪ§yЃН![]() ЃЈnЁй0ЃЌxЃО0ЃЉЕФЭМЯѓЙ§ЕуAЃЈ3ЃЌ2ЃЉЃЌгыжБЯпlЃКyЃНkx+bНЛгкЕуCЃЌжБЯпlгыyжсНЛгкЕуBЃЈ0ЃЌЉ1ЃЉЃЎ
ЃЈnЁй0ЃЌxЃО0ЃЉЕФЭМЯѓЙ§ЕуAЃЈ3ЃЌ2ЃЉЃЌгыжБЯпlЃКyЃНkx+bНЛгкЕуCЃЌжБЯпlгыyжсНЛгкЕуBЃЈ0ЃЌЉ1ЃЉЃЎ
ЃЈ1ЃЉЧѓnЁЂbЕФжЕЃЛ
ЃЈ2ЃЉКсЁЂзнзјБъЖМЪЧећЪ§ЕФЕуНазіећЕуЃЎМЧКЏЪ§yЃН![]() ЃЈnЁй0ЃЌxЃО0ЃЉЕФЭМЯѓдкЕуAЃЌCжЎМфЕФВПЗжгыЯпЖЮBAЃЌBCЮЇГЩЕФЧјгђЃЈВЛКЌБпНчЃЉЮЊWЃЎ
ЃЈnЁй0ЃЌxЃО0ЃЉЕФЭМЯѓдкЕуAЃЌCжЎМфЕФВПЗжгыЯпЖЮBAЃЌBCЮЇГЩЕФЧјгђЃЈВЛКЌБпНчЃЉЮЊWЃЎ
ЂйЕБжБЯпlЙ§ЕуЃЈ2ЃЌ0ЃЉЪБЃЌжБНгаДГіЧјгђWФкЕФећЕуИіЪ§ЃЌВЂаДГіЧјгђWФкЕФећЕуЕФзјБъЃЛ
ЂкШєЧјгђWФкЕФећЕуВЛЩйгк5ИіЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОйАьЧђШќЃЌЗжЮЊШєИЩзщЃЌЦфжаЕквЛзщгаAЃЌBЃЌCЃЌDЃЌEЮхИіЖгЃЎетЮхИіЖгвЊНјааЕЅбЛЗШќЃЌМДУПСНИіЖгжЎМфвЊНјаавЛГЁБШШќЃЌУПГЁБШШќВЩгУШ§ОжСНЪЄжЦЃЌМДШ§ОжжаЪЄСНОжОЭЛёЪЄЃЎУПГЁБШШќЪЄИКЫЋЗНИљОнБШЗжЛсЛёЕУЯргІЕФЛ§ЗжЃЌЛ§ЗжОљЮЊе§ећЪ§ЃЎетЮхИіЖгЭъГЩЫљгаБШШќКѓЕУЕНШчЯТЕФЛ§ЗжБэЃЎ
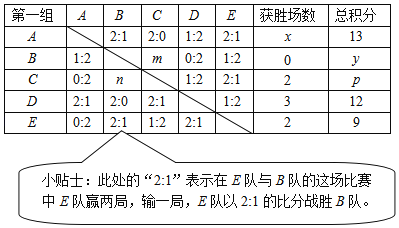
ИљОнЩЯБэЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕквЛзщвЛЙВНјааСЫЁЁ ЁЁГЁБШШќЃЌAЖгЕФЛёЪЄГЁЪ§xЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЕБBЖгЕФзмЛ§Зжy=6ЪБЃЌЩЯБэжаmДІгІЬюЁЁ ЁЁЃЌnДІгІЬюЁЁ ЁЁЃЛ
ЃЈ3ЃЉаДГіCЖгзмЛ§ЗжpЕФЫљгаПЩФмжЕЮЊЃКЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌlЪЧОЙ§AЃЈ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌbЃЉСНЕуЕФжБЯпЃЌЧвb0ЃЌЕуCЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЕБЕуBвЦЖЏЪБЃЌЙ§ЕуCзїCDЁЭlНЛгкЕуDЃЎ
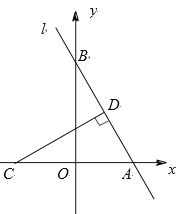
ЃЈ1ЃЉЧѓЕуDЃЌOжЎМфЕФОрРыЃЛ
ЃЈ2ЃЉЕБtanЁЯCDO=![]() ЪБЃЌЧѓжБЯпlЕФНтЮіЪНЃЛ
ЪБЃЌЧѓжБЯпlЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌжБНгаДГіЁїACDгыЁїAOBжиЕўВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвЭЦааЁАНкФмМѕХХЃЌЕЭЬМОМУЁБеўВпКѓЃЌЕЭХХСПЕФЦћГЕБШНЯГЉЯњЃЌФГЦћГЕОЯњЩЬЙКНјAЁЂBСНжжаЭКХЕФЕЭХХСПЦћГЕЃЌЦфжаAаЭЦћГЕЕФНјЛѕЕЅМлБШBаЭЦћГЕЕФНјЛѕЕЅМлЖр2ЭђдЊЃЛЛЈ50ЭђдЊЙКНјAаЭЦћГЕЕФЪ§СПгыЛЈ40ЭђдЊЙКНјBаЭЦћГЕЕФЪ§СПЯрЭЌЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНжжаЭКХЦћГЕЕФНјЛѕЕЅМлЃЛ
ЃЈ2ЃЉЯњЪлжаЗЂЯжAаЭЦћГЕЕФУПжмЯњСПyAЃЈЬЈЃЉгыЪлМлxЃЈЭђдЊ/ЬЈЃЉТњзуКЏЪ§ЙиЯЕyAЃНЉx+20ЃЌBаЭЦћГЕЕФУПжмЯњСПyBЃЈЬЈЃЉгыЪлМлxЃЈЭђдЊ/ЬЈЃЉТњзуКЏЪ§ЙиЯЕyBЃНЉx+14ЃЌAаЭЦћГЕЕФЪлМлБШBаЭЦћГЕЕФЪлМлИп2ЭђдЊ/ЬЈЃЎЮЪAЁЂBСНжжаЭКХЕФЦћГЕЪлМлИїЮЊЖрЩйЪБЃЌУПжмЯњЪлетСНжжЦћГЕЕФзмРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
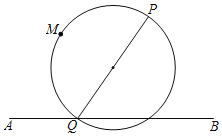
ЁОЬтФПЁПШчЭМЃЌЦНУцЩЯДцдкЕуPЁЂЕуMгыЯпЖЮABЃЎШєЯпЖЮABЩЯДцдквЛЕуQЃЌЪЙЕУЕуMдквдPQЮЊжБОЖЕФдВЩЯЃЌдђГЦЕуMЮЊЕуPгыЯпЖЮABЕФЙВдВЕуЃЎ
вбжЊЕуPЃЈ0ЃЌ1ЃЉЃЌЕуAЃЈЉ2ЃЌЉ1ЃЉЃЌЕуBЃЈ2ЃЌЉ1ЃЉЃЎ
ЃЈ1ЃЉдкЕуOЃЈ0ЃЌ0ЃЉЃЌCЃЈЉ2ЃЌ1ЃЉЃЌDЃЈ3ЃЌ0ЃЉжаЃЌПЩвдГЩЮЊЕуPгыЯпЖЮABЕФЙВдВЕуЕФЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЕуKЮЊxжсЩЯвЛЕуЃЌШєЕуKЮЊЕуPгыЯпЖЮABЕФЙВдВЕуЃЌЧыЧѓГіЕуKКсзјБъxKЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉвбжЊЕуMЃЈmЃЌЉ1ЃЉЃЌШєжБЯпyЃН![]() x+3ЩЯДцдкЕуPгыЯпЖЮAMЕФЙВдВЕуЃЌЧыжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
x+3ЩЯДцдкЕуPгыЯпЖЮAMЕФЙВдВЕуЃЌЧыжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com