
����Ŀ��С����С�ϲμ���100m�ܵ�5�ڼ�ѵ��ÿ�ڼ�ѵ����ʱ���в��ԣ��������ǵļ�ѵʱ�䡢���Գɼ����Ƴ���ͼ����ͳ��ͼ��
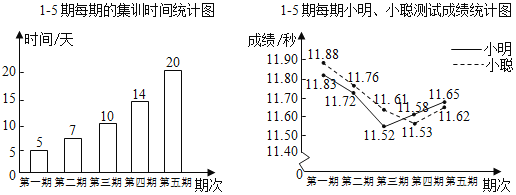
����ͼ����Ϣ���������ĸ��ƶϣ�
����5�ڵļ�ѵ����56�죻
��С��5�β��Ե�ƽ���ɼ���11.68�룻
�۴Ӽ�ѵʱ�俴����ѵʱ�䲻��Խ��Խ�ã���ѵʱ�����������������ۣ����³ɼ��»���
�ܴӲ��Գɼ��������˵���óɼ������ڵ�4�ڳ��֣����鼯ѵʱ�䶨Ϊ14�죮
���к����ƶϵ�����ǣ�������
A.�٢�B.�ڢ�C.�ڢ�D.�٢�
���𰸡�A
��������
��������ͳ��ͼ��ÿ�ڵ�������Ӽ��ɵõ���5�ڵļ�ѵ���ж����죻��������ͳ��ͼ�������С��5�β��Ե�ƽ���ɼ�������ͼ�е���Ϣ�������֪��ƽ���ɼ�������ڵ�1�ڣ�
�⣺���ڢ٣���5�ڵļ�ѵ����5+7+10+14+20��56���죩������ȷ��
���ڢڣ�С��5�β��Ե�ƽ���ɼ��ǣ���11.83+11.72+11.52+11.58+11.65����5��11.66���룩���ʴ���
���ڢۣ��Ӽ�ѵʱ�俴����ѵʱ�䲻��Խ��Խ�ã���ѵʱ�����������������ۣ����³ɼ��»�������ȷ��
���ڢܣ��Ӳ��Գɼ��������˵���õ�ƽ���ɼ����ڵ�1�ڳ��֣����鼯ѵʱ�䶨Ϊ5�죮�ʴ���
��ѡ��A��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ䣬�ס��ҡ�������4��ͬѧԼ����һ������ÿ����һ�鸩�Գţ�Ϊ������Ȥζ�ԣ�����ͨ����Ϸ��ʽȷ��ÿ����ÿ���ѵ���ƻ���
���ȣ�����ͼ��ʽ�ڷ����ſ�Ƭ��������в�ͬ�����ִ���ÿ�������Գŵĸ������������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ڼ�¼��
���ڼ�¼��
![]()
������Ϸ�������£�
��ͬѧ��ͬʱ����![]() ��
��![]() �����������ֽ��бȽϣ�Ȼ����С�����¼�ڱ����У�
�����������ֽ��бȽϣ�Ȼ����С�����¼�ڱ����У�![]() ��
��![]() ��
��![]() ��ԭ˳���¼�ڱ����У�
��ԭ˳���¼�ڱ����У�
��ͬѧ��ͬʱ����![]() ��
��![]() ��
��![]() �����������ֽ��бȽϣ�Ȼ����С�����¼�ڱ����У�
�����������ֽ��бȽϣ�Ȼ����С�����¼�ڱ����У�![]() ��
��![]() ��ԭ˳���¼�ڱ����У�
��ԭ˳���¼�ڱ����У�
�Դ����ƣ�����ͬѧʱ�����ſ�Ƭȫ������������С�����¼�ڱ����У�
�±���¼����������ͬѧ�����ѵ���ƻ���
����һ | ���ڶ� | ������ | ������ | ������ | |
��ͬѧ |
|
|
|
|
|
��ͬѧ |
|
|
|
|
|
��ͬѧ | |||||
��ͬѧ |
|
|
|
|
|
���ݼ�¼���������⣺
��1����ȫ�ϱ��б�ͬѧ��ѵ���ƻ���
��2����֪ÿ��ͬѧÿ��������30�������������180����
�����![]() ��
��![]() ����ô
����ô![]() ���п���ȡֵΪ__________________________��
���п���ȡֵΪ__________________________��
��������ͬѧ����_________�����Գŵ��ܸ�����࣬�ܸ������Ϊ_________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
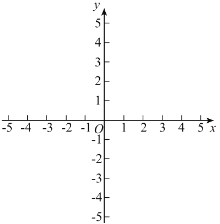
����Ŀ����ƽ��ֱ������ϵ![]() �У�����������
�У�����������![]() �Լ�����
�Լ�����![]() ��
��
(1)��������ߵĶ������ꣻ(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
(2)���������߾�����![]() ����������ߵı���ʽ��
����������ߵı���ʽ��
(3)�������������߶�![]() �й����㣬���ͼ����
�й����㣬���ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����־�ɳǣ��������飬������������ijУijС��7��ͬѧ��������Լ����㻨Ǯ֧Ԯ���������Ǿ�������ֱ��ǣ���λ��Ԫ����100��45��100��40��100��60��155���������ĸ��ƶϣ�
����7��ͬѧ������㻨Ǯ��ƽ������150��
����7��ͬѧ������㻨Ǯ����λ����100��
����7��ͬѧ������㻨Ǯ��������100��
������7��ͬѧ������㻨Ǯ����λ����100�������ƶϸ�Уȫ��ͬѧ������㻨Ǯ����λ��Ҳһ����100��
���к����ƶϵ�����ǣ� ��
A.�٢�B.�ڢ�C.�ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��x2��2mx+m��4��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��0����3����
��1����m��ֵ��
��2����һ�κ���y��kx+5��k��0����ͼ����A����k��ֵ��
��3�������κ�����ͼ���ڵ�B��C��IJ��֣�����B�͵�C������ƽ��n��n��0������λ��õ���ͼ���ΪG��ͬʱ����2���еõ���ֱ��y��kx+5��k��0������ƽ��n����λ����ƽ�ƺ��ֱ����ͼ��G�й�����ʱ������ͼ��ֱ��д��n��ȡֵ��Χ��
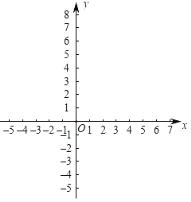
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��11�£������о�ԺЯ��֪ʶ��Ȩ��ƴ���ƽ̨��ۣ����Ϸ�����IP��ȼAI�¼�Ԫ��2019�й��˹����ܲ�ҵ֪ʶ��Ȩ��չ��Ƥ�顷����Ƥ�鹫����2019�й��˹�������ҵ֪ʶ��Ȩ��������ǿ��500����й��˹�����������ҵ���ж�������������100�֣���ǰ�����ֱ�Ϊ����Ϊ����Ѷ���ٶȣ��Ե÷��ɸߵ��͵�ǰ41����ҵ���й����ݽ����ռ��������������ͷ�������������˲�����Ϣ��
a���÷ֵ�Ƶ���ֲ�ֱ��ͼ��
�����ݷֳ�8�飺60��x��65��65��x��70��70��x��75��75��x��80��80��x��85��85��x��90��90��x��95��95��x��100����
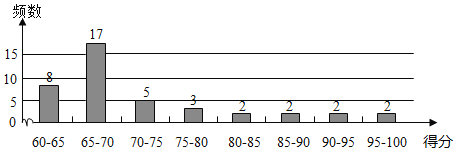
b��֪ʶ��Ȩ�������÷���70��x��75��һ����ǣ�70.3��71.6��72.1��72.5��74.1��
c��41����ҵע�����ڳ��зֲ�ͼ������������ͼ�����������һλС����
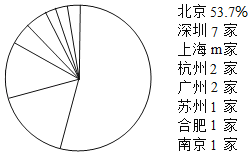
d�������Ƽ��ɷ�����˾��֪ʶ��Ȩ�������÷���70.3��
������������Դ�ڡ�IP��ȼAI�¼�Ԫ��2019�й��˹����ܲ�ҵ֪ʶ��Ȩ��չ��Ƥ�顷��
����������Ϣ���ش��������⣺
��1�������Ƽ��ɷ�����˾��֪ʶ��Ȩ�������÷������ǵ��� ����
��2���ٶ����˹���������ȡ�����ɹ������������ܼҾӡ��Զ���ʻ���������ҵ�����������ٶȶ��ѽ���ǰհ���֣�������ưٶ��ڱ������а��еĵ÷ִ������ ����
��3����41����ҵע�����ڳ��зֲ�ͼ�У�m���� ����������Ӱ��������Ϻ�������
��4�������ƶϺ��������� ������ֻ����ţ�
��ǰ41����ҵ��֪ʶ��Ȩ�������÷ֵ���λ��Ӧ��65��x��70��һ���У�������65��x��70��һ��Ŀ��������
��ǰ41����ҵ�ֲ����ҹ�8�����У��˹����ܲ�ҵ�ķ�չ�ۼ��ھ��á��Ƽ���������Է���ij��У�һ�߳����У���������������ͻ�������װ������ҵ��������ֱ������˹���������IJ�ҵ��Ⱥ���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ı�����һ��Ա�ƽ�У�����һ��Ա߲�ƽ�У���ô���������ı���Ϊ���Σ�����������һ������ֱ�ǣ������Ϊֱ�����Σ������ĸ������У�
�ٴ���������ֱ�����Σ����ĸ�����ֱ���ͬһ�������ε��������ϣ�
�ڴ���������ֱ�����Σ����ĸ�������ͬһ���������ϣ�
�۴���������ֱ�����Σ����ĸ�������ͬһ��������������ͼ���ϣ�
�����ٴ���һ��ֱ�����Σ����ĸ�������ͬһ��Բ�ϣ�
������ȷ���۵������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�ڣ������ű߳��ֱ�Ϊa��b��a��b����������ֽƬ��ͼ1��ͼ2���ַ�ʽ���ã�ͼ1��ͼ2������������ֽƬ���в����ص�����������δ��������������ֽƬ���ǵIJ�������Ӱ��ʾ����ͼ2����Ӱ���ֵ��ܳ���ͼ1����Ӱ���ֵ��ܳ��IJ�Ϊl����Ҫ֪��l��ֵ��ֻҪ����ͼ�������߶εij���������
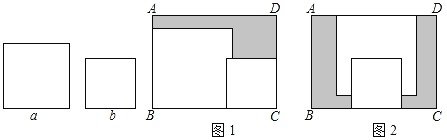
A.aB.bC.ADD.AB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���������������������PAB����PCD��_____��������A��B��C��D��P�������߽��㣩
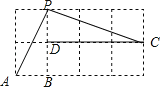
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com