
【题目】如图所示的网格是正方形网格,则∠PAB﹣∠PCD=_____°.(点A,B,C,D,P是网格线交点)
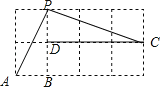
【答案】45
【解析】
连接AE,PE,由图可知,∠EAB=∠PCD,则∠PAB∠PCD=∠PAB∠EAB=∠PAE,然后根据勾股定理可以求得PA、PE、AE的长,再利用勾股定理的逆定理可以判断△PAE的形状,从而可以得到∠PAE的度数,然后即可得到∠PAB∠PCD的度数.
解:连接AE,PE,
则∠EAB=∠PCD,
故∠PAB﹣∠PCD=∠PAB﹣∠EAB=∠PAE,
设正方形网格的边长为a,
则PA=![]() ,PE=
,PE=![]() ,AE=
,AE=![]() ,
,
∵PA2+PE2=5a2+5a2=10a2=AE2,
∴△APE是直角三角形,∠APE=90°,
又∵PA=PE,
∴∠PAE=∠PEA=45°,
∴∠PAB﹣∠PCD=45°,
故答案为:45.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】小明、小聪参加了100m跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如图两个统计图.
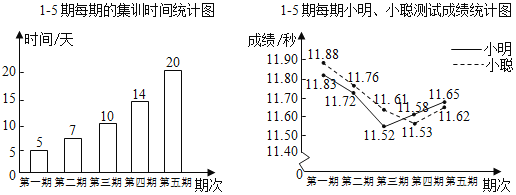
根据图中信息,有下面四个推断:
①这5期的集训共有56天;
②小明5次测试的平均成绩是11.68秒;
③从集训时间看,集训时间不是越多越好,集训时间过长,可能造成劳累,导致成绩下滑;
④从测试成绩看,两人的最好成绩都是在第4期出现,建议集训时间定为14天.
所有合理推断的序号是( )
A.①③B.②④C.②③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“生成三角形”.
(1)已知点A(4,0);
①若以线段OA为底的某等腰三角形恰好是点O,A的“生成三角形”,求该三角形的腰长;
②若Rt△ABC是点A,B的“生成三角形”,且点B在x轴上,点C在直线y=2x﹣5上,则点B的坐标为 ;
(2)⊙T的圆心为点T(2,0),半径为2,点M的坐标为(2,6),N为直线y=x+4上一点,若存在Rt△MND,是点M,N的“生成三角形”,且边ND与⊙T有公共点,直接写出点N的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
(1)求k及点B的坐标;
(2)若点C是y轴上一点,且S△ABC=5,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
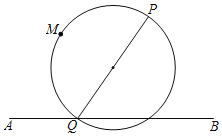
【题目】如图,平面上存在点P、点M与线段AB.若线段AB上存在一点Q,使得点M在以PQ为直径的圆上,则称点M为点P与线段AB的共圆点.
已知点P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
(1)在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是 ;
(2)点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;
(3)已知点M(m,﹣1),若直线y=![]() x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质并解决问题.
的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)取几组![]() 与
与![]() 的对应值,填写在下表中.
的对应值,填写在下表中.
| … |
|
|
| 0 | 1 | 1.2 | 1.25 | 2.75 | 2.8 | 3 | 4 | 5 | 6 | 8 | … |
| … | 1 | td style="width:6%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">2 | 3 | 6 | 7.5 | 8 | 8 | 7.5 | 6 | 3 |
| 1.5 | 1 | … |
![]() 的值为_____________;
的值为_____________;
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
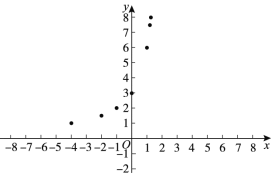
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数![]() 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;
②过点![]() 作直线
作直线![]() 轴,与函数
轴,与函数![]() 的图象交于点
的图象交于点![]() (点
(点![]() 在点
在点![]() 的左侧),则
的左侧),则![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
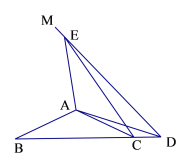
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
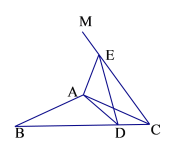
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com