
【题目】已知:在平面直角坐标系xOy中,函数y=![]() (n≠0,x>0)的图象过点A(3,2),与直线l:y=kx+b交于点C,直线l与y轴交于点B(0,﹣1).
(n≠0,x>0)的图象过点A(3,2),与直线l:y=kx+b交于点C,直线l与y轴交于点B(0,﹣1).
(1)求n、b的值;
(2)横、纵坐标都是整数的点叫做整点.记函数y=![]() (n≠0,x>0)的图象在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
(n≠0,x>0)的图象在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点(2,0)时,直接写出区域W内的整点个数,并写出区域W内的整点的坐标;
②若区域W内的整点不少于5个,结合函数图象,求k的取值范围.
【答案】(1)n=6,b=﹣1;(2)①(3,1),②0<k<![]() 或k>5
或k>5
【解析】
(1)把A(3,2)代入y=![]() (n≠0,x>0)中可得n的值;把点B(0,﹣1)代入y=kx+b中可得b的值;
(n≠0,x>0)中可得n的值;把点B(0,﹣1)代入y=kx+b中可得b的值;
(2)①将(2,0)代入y=kx﹣1可得:直线解析式为y=![]() x﹣1,画图可得整点的个数;
x﹣1,画图可得整点的个数;
②分两种情况:直线l在OA的下方和上方,画图计算边界时k的值,可得k的取值.
解:(1)∵点A(3,2)在函数![]() 的图象上,
的图象上,
∴n=6,
∵点B(0,﹣1)在直线l:y=kx+b上,
∴b=﹣1;
(2)①当直线l过点(2,0)时,直线解析式为y=![]() x﹣1,
x﹣1,
解方程![]() =
=![]() x﹣1得x1=1﹣
x﹣1得x1=1﹣![]() (舍去),x2=1+
(舍去),x2=1+![]() ,则C(1+
,则C(1+![]() ,
,![]() ),
),
而B(0,﹣1),
如图1所示,区域W内的整点有(3,1)一个;
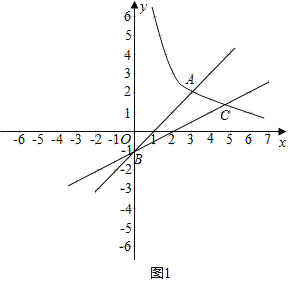
②(ⅰ)当直线l在BA下方时,
若直线l与x轴交于点(3,0),结合图象,区域W内有4个整点,
此时:3k﹣1=0,
∴![]() .
.
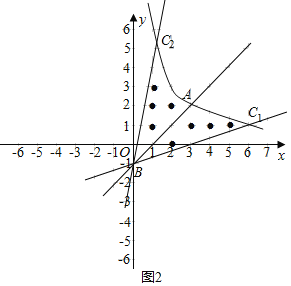
当直线l与x轴的交点在(3,0)右侧时,区域W内整点个数不少于5个,
∴0<k<![]() .
.
(ⅱ)当直线l在BA上方时,若直线l过点(1,4),结合图象,区域W内有4个整点,
此时k﹣1=4,解得 k=5.
结合图象,可得 k>5时,区域W内整点个数不少于5个,
综上,k的取值范围是0<k<![]() 或k>5.
或k>5.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y1=x(x<m)的图象与函数y2=x2(x≥m)的图象组成图形G.对于任意实数n,过点P(0,n)且与x轴平行的直线总与图形G有公共点,写出一个满足条件的实数m的值为_____(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m﹣4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
(1)求m的值;
(2)若一次函数y=kx+5(k≠0)的图象经过点A,求k的值;
(3)将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+5(k≠0)向上平移n个单位,当平移后的直线与图象G有公共点时,请结合图象直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
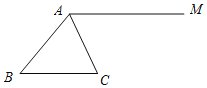
【题目】如图,AM∥BC,且AC平分∠BAM.
(1)用尺规作∠ABC的平分线BD交AM于点D,连接CD.(只保留作图痕迹,不写作法)
(2)求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果四边形有一组对边平行,且另一组对边不平行,那么称这样的四边形为梯形,若梯形中有一个角是直角,则称其为直角梯形.下面四个结论中:
①存在无数个直角梯形,其四个顶点分别在同一个正方形的四条边上;
②存在无数个直角梯形,其四个顶点在同一条抛物线上;
③存在无数个直角梯形,其四个顶点在同一个反比例函数的图象上;
④至少存在一个直角梯形,其四个顶点在同一个圆上.
所有正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=α,A为射线OM上一定点,OA=5,B为射线ON上一动点,连接AB,满足∠OAB,∠OBA均为锐角.点C在线段OB上(与点O,B不重合),满足AC=AB,点C关于直线OM的对称点为D,连接AD,OD.
(1)依题意补全图1;
(2)求∠BAD的度数(用含α的代数式表示);
(3)若tanα=![]() ,点P在OA的延长线上,满足AP=OC,连接BP,写出一个AB的值,使得BP∥OD,并证明.
,点P在OA的延长线上,满足AP=OC,连接BP,写出一个AB的值,使得BP∥OD,并证明.
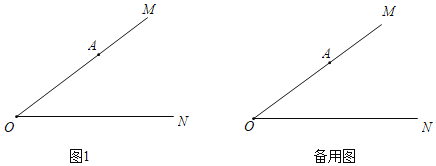
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函教表达式为y=kx+6.
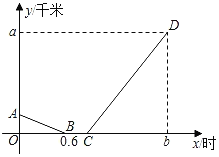
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
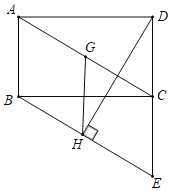
【题目】如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC中点,连接GH.
(1)求证:BE=AC.
(2)判断GH与BE的数量关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com