
【题目】北京某超市按月订购一种酸奶,每天的进货量相同.根据往年的销售经验,每天需求量与当天最高气温(单位:℃)有关.为了确定今年六月份的酸奶订购计划,对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析,下面给出了部分信息.
a.酸奶每天需求量与当天最高气温关系如表:
最高气温t(单位:℃) | 20≤t<25 | 25≤t<30 | 30≤t≤40 |
酸奶需求量(单位:瓶/天) | 300 | 400 | 600 |
b.2017年6月最高气温数据的频数分布统计表如表(不完整):
2017年6月最高气温数据的频数分布表:
分组 | 频数 | 频率 |
20≤t<25 | 3 | |
25≤t<30 | m | 0.20 |
30≤t<35 | 14 | |
35≤t≤40 | 0.23 | |
合计 | 30 | 1.00 |
c.2018年6月最高气温数据的频数分布直方图如图:
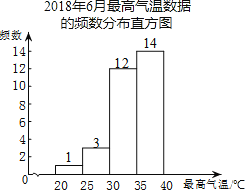
d.2019年6月最高气温数据如下(未按日期顺序):
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
根据以上信息,回答下列问题:
(1)m的值为 ;
(2)2019年6月最高气温数据的众数为 ,中位数为 ;
(3
(4)已知该酸奶进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.
①2019年6月这种酸奶每天的进货量为500瓶,则此月这种酸奶的利润为 元;
②根据以上信息,预估2020年6月这种酸奶订购的进货量不合理的为 .
A.550瓶/天
B.600瓶/天
C.380瓶/天
【答案】(1)6;(2)32,32.5;(3)![]() ;(4)①28000,②C
;(4)①28000,②C
【解析】
(1)估计频数=总数×频率即可得到结论;
(2)估计众数和中位数的定义即可得到结论;
(3)估计概率公式计算即可;
(4)根据题意列式计算即可得到结论.
解:(1)m=30×0.20=6;
(2)2019年6月最高气温数据的众数为32,中位数为![]() =32.5;
=32.5;
(3)三年这种酸奶一天的需求量为600瓶的天数为21+26+25=72,
估计六月份这种酸奶一天的需求量为600瓶的概率为![]() =
=![]() ;
;
(4)①400×(6﹣4)×5+(500﹣400)×(2﹣4)×5+500×(6﹣4)×25=28000;
②∵以上三年6月最高气温低于25的天数一共有3+1=4天,
∴有86天酸奶每天需求量大于400瓶,
故预估2020年6月这种酸奶订购的进货量不合理的为C,
故选C.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
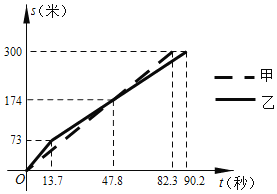
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,根据图象有以下四个判断:
①乙队率先到达终点;
②甲队比乙队多走了126米;
③在47.8秒时,两队所走路程相等;
④从出发到13.7秒的时间段内,甲队的速度比乙队的慢.
所有正确判断的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为等边三角形.
为等边三角形.
(1)求作:![]() 的外接圆
的外接圆![]() .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
(2)射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() .
.
①根据题意,将(1)中图形补全;
②求证:![]() ;
;
③若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,存在抛物线
中,存在抛物线![]() 以及两点
以及两点![]() .
.
(1)求该抛物线的顶点坐标;(用含![]() 的代数式表示)
的代数式表示)
(2)若该抛物线经过点![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)若该抛物线与线段![]() 有公共点,结合图象,求
有公共点,结合图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y1=x(x<m)的图象与函数y2=x2(x≥m)的图象组成图形G.对于任意实数n,过点P(0,n)且与x轴平行的直线总与图形G有公共点,写出一个满足条件的实数m的值为_____(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】众志成城,抗击疫情,救助重灾区.某校某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):100,45,100,40,100,60,155.下面有四个推断:
①这7名同学所捐的零花钱的平均数是150;
②这7名同学所捐的零花钱的中位数是100;
③这7名同学所捐的零花钱的众数是100;
④由这7名同学所捐的零花钱的中位数是100,可以推断该校全体同学所捐的零花钱的中位数也一定是100.
所有合理推断的序号是( )
A.①③B.②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m﹣4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
(1)求m的值;
(2)若一次函数y=kx+5(k≠0)的图象经过点A,求k的值;
(3)将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+5(k≠0)向上平移n个单位,当平移后的直线与图象G有公共点时,请结合图象直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果四边形有一组对边平行,且另一组对边不平行,那么称这样的四边形为梯形,若梯形中有一个角是直角,则称其为直角梯形.下面四个结论中:
①存在无数个直角梯形,其四个顶点分别在同一个正方形的四条边上;
②存在无数个直角梯形,其四个顶点在同一条抛物线上;
③存在无数个直角梯形,其四个顶点在同一个反比例函数的图象上;
④至少存在一个直角梯形,其四个顶点在同一个圆上.
所有正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y![]() 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若![]() ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com