
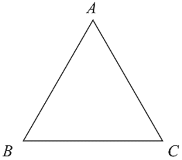
【题目】已知:![]() 为等边三角形.
为等边三角形.
(1)求作:![]() 的外接圆
的外接圆![]() .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
(2)射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() .
.
①根据题意,将(1)中图形补全;
②求证:![]() ;
;
③若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①见解析;②见解析;③EF=![]() .
.
【解析】
(1)直接利用外接圆的作法作出三角形任意两边的垂直平分线,进而得出外接圆圆心,进而得出答案;
(2)①按题意画出图形即可;
②连接OB,OC,证明AE⊥BC.可得出AE⊥EF,则结论得证;
③得出∠BOD=60°,设OD=x,则OB=OE=2+x,得出cos∠BOD=![]() ,求出x=2,得出tan∠BAD=
,求出x=2,得出tan∠BAD=![]() ,则可求出EF的值.
,则可求出EF的值.
解:(1)如图所示:⊙O即为所求.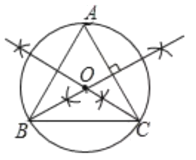
(2)①如图,补全图形: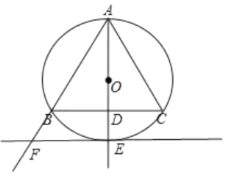
②证明:连接OB,OC,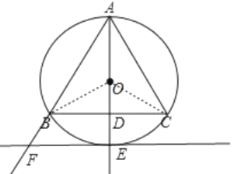
∵OB=OC,
∴点O在线段BC的垂直平分线上,
∵△ABC为等边三角形,
∴AB=AC,
∴点A在线段BC的垂直平分线上,
∴AO垂直平分BC,
∴AE⊥BC.
∵直线EF为⊙O的切线,
∴AE⊥EF,
∴EF∥BC;
③∵△ABC为等边三角形,
∴∠BAC=60°,
∵AB=AC,AE⊥BC,
∴∠BAD=![]() ∠BAC,
∠BAC,
∴∠BAD=30°,
∴∠BOD=60°,
∵DE=2,
设OD=x,
∴OB=OE=2+x,
在Rt△OBD中,∵OD⊥BC,∠BOD=60°,
∴cos∠BOD=![]() ,
,
∴x=2,
∴OD=2,OB=4,
∴AE=8,
在△AEF中,∵AE⊥EF,∠BAD=30°,
∴tan∠BAD=![]() ,
,
∴EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】随着智能手机的普及,“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐,某商场对2019年712月中使用这两种手机支付方式的情况进行统计,得到如图所示的折线图,根据统计图中的信息,得出以下四个推断,其中不合理的是( )
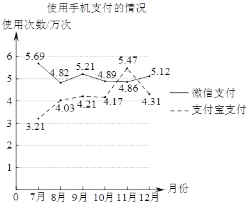
A.6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多;
B.6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大;
C.6个月中11月份使用手机支付的总次数最多;
D.9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,![]() 社区有500名在职党员,为了解本社区2月-3月期间在职党员参加应急执勤的情况,
社区有500名在职党员,为了解本社区2月-3月期间在职党员参加应急执勤的情况,![]() 社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
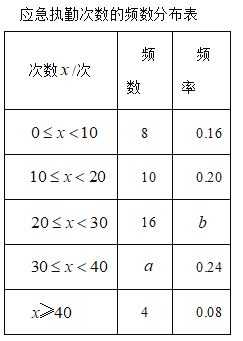
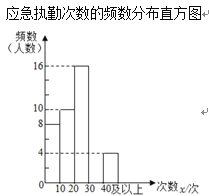
其中,应急执勤次数在![]() 这一组的数据是:
这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() ______,
______,![]() ______;
______;
(2)请补全频数分布直方图;
(3)随机抽取的50名在职党员参加应急执勤次数的中位数是______;
(4)请估计2月-3月期间![]() 社区在职党员参加应急执勤的次数不低于30次的约有______人.
社区在职党员参加应急执勤的次数不低于30次的约有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一笔总额为![]() 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给
元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给![]() 个人,评一、二、三等奖的人数分别为
个人,评一、二、三等奖的人数分别为![]() ,且
,且![]() ,那么三等奖的奖金金额是_______元.
,那么三等奖的奖金金额是_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 的两边上(不与点
的两边上(不与点![]() 重合),并且
重合),并且![]() 除端点外的所有点都在
除端点外的所有点都在![]() 的内部,则称
的内部,则称![]() 是
是![]() 的“连角弧”.
的“连角弧”.
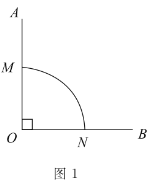
(1)图1中,![]() 是直角,
是直角,![]() 是以
是以![]() 为圆心,半径为1的“连角弧”.
为圆心,半径为1的“连角弧”.
①图中![]() 的长是______,并在图中再作一条以
的长是______,并在图中再作一条以![]() 为端点、长度相同的“连角弧”;
为端点、长度相同的“连角弧”;
②以![]() 为端点,弧长最长的“连角弧”的长度是_______.
为端点,弧长最长的“连角弧”的长度是_______.
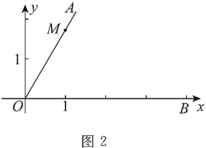
(2)如图2,在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴正半轴上,若
轴正半轴上,若![]() 是半圆,也是
是半圆,也是![]() 的“连角弧”,求
的“连角弧”,求![]() 的取值范围.
的取值范围.
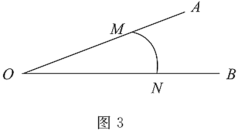
(3)如图3,已知点![]() 分别在射线
分别在射线![]() 上,
上,![]() 是
是![]() 的“连角弧”,且
的“连角弧”,且![]() 所在圆的半径为
所在圆的半径为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京某超市按月订购一种酸奶,每天的进货量相同.根据往年的销售经验,每天需求量与当天最高气温(单位:℃)有关.为了确定今年六月份的酸奶订购计划,对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析,下面给出了部分信息.
a.酸奶每天需求量与当天最高气温关系如表:
最高气温t(单位:℃) | 20≤t<25 | 25≤t<30 | 30≤t≤40 |
酸奶需求量(单位:瓶/天) | 300 | 400 | 600 |
b.2017年6月最高气温数据的频数分布统计表如表(不完整):
2017年6月最高气温数据的频数分布表:
分组 | 频数 | 频率 |
20≤t<25 | 3 | |
25≤t<30 | m | 0.20 |
30≤t<35 | 14 | |
35≤t≤40 | 0.23 | |
合计 | 30 | 1.00 |
c.2018年6月最高气温数据的频数分布直方图如图:
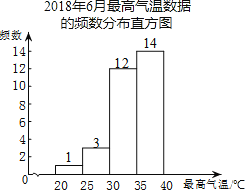
d.2019年6月最高气温数据如下(未按日期顺序):
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
根据以上信息,回答下列问题:
(1)m的值为 ;
(2)2019年6月最高气温数据的众数为 ,中位数为 ;
(3
(4)已知该酸奶进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.
①2019年6月这种酸奶每天的进货量为500瓶,则此月这种酸奶的利润为 元;
②根据以上信息,预估2020年6月这种酸奶订购的进货量不合理的为 .
A.550瓶/天
B.600瓶/天
C.380瓶/天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
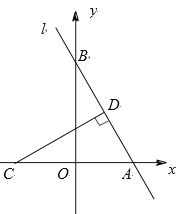
(1)求点D,O之间的距离;
(2)当tan∠CDO=![]() 时,求直线l的解析式;
时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com