
【题目】下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程.
已知:![]() 中,
中,![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ,
,![]() 和
和![]() 交于点
交于点![]() ;
;
③连接![]() 和
和![]() ;
;
④以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() .
.
所以![]() .
.
根据小菲设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);

(2)完成下面的证明.

证明:连接![]()
∵![]() 和
和![]() 分别为
分别为![]() 、
、![]() 的垂直平分线,
的垂直平分线,
∴![]() ________.
________.
∴![]() 是
是![]() 的外接圆.
的外接圆.
∵点![]() 是
是![]() 上的一点,
上的一点,
∴![]() .(____________).(填推理的依据)
.(____________).(填推理的依据)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表:
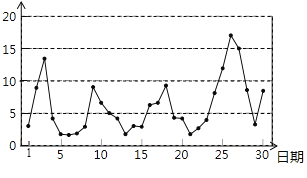
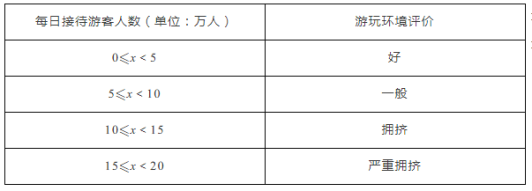
根据以上信息,以下四个判断中,正确的是_________.(填写所有正确结论的序号)
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10广域网人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
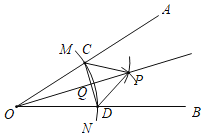
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进城乡生活垃圾分类的行动中,为了了解社区居民对垃圾分类知识的掌握情况,某社区随机抽取40名居民进行测试,并对他们的得分数据进行收集、整理、描述和分析.下面给出了部分信息:
a.社区40名居民得分的频数分布直方图:(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100):
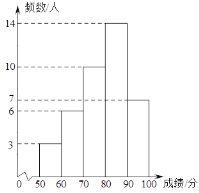
b.社区居民得分在80≤x<90这一组的是:
80 80 81 82 83 84 84 85 85 85 86 86 87 89
c.40个社区居民的年龄和垃圾分类知识得分情况统计图:
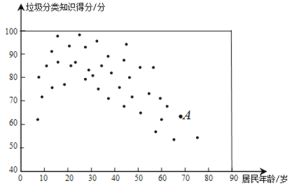
d.社区居民甲的垃圾分类知识得分为89分.
根据以上信息,回答下列问题:
(1)社区居民甲的得分在抽取的40名居民得分中从高到低排名第 ;
(2)在垃圾分类得分比居民甲得分高的居民中,居民年龄最大约是 岁;
(3)下列推断合理的是 .
①相比于点A所代表的社区居民,居民甲的得分略高一些,说明青年人比老年人垃圾分类知识掌握得更好一些;
②垃圾分类知识得分在90分以上的社区居民年龄主要集中在15岁到35岁之间,说明青年人垃圾分类知识掌握更为全面,他们可以向身边的老年人多宣传垃圾分类知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意点![]() ,如果满足
,如果满足![]() (x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(1)当2≤a≤3时,
①在点![]() 中,满足此条件的特征点为__________________;
中,满足此条件的特征点为__________________;
②⊙W的圆心为![]() ,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
(2)已知函数![]() ,请利用特征点求出该函数的最小值.
,请利用特征点求出该函数的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 在射线
在射线![]() 上,点
上,点![]() 是射线
是射线![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合).点
重合).点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 、
、![]() 和
和![]() ,点
,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .小明在探究图形运动的过程中发现:
.小明在探究图形运动的过程中发现:![]() 始终成立.
始终成立.

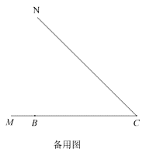
(1)如图1,当![]() 时;
时;
①求证:![]() ;
;
②用等式表示线段![]() 、
、![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)当![]() 时,直接用等式表示线段
时,直接用等式表示线段![]() 、
、![]() 与
与![]() 之间的数量关系是______.
之间的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P为图形M上任意一点,点Q为图形N上任意一点,若点P与点Q之间的距离PQ始终满足PQ>0,则称图形M与图形N相离.
(1)已知点A(1,2)、B(0,﹣5)、C(2,﹣1)、D(3,4).
①与直线y=3x﹣5相离的点是 ;
②若直线y=3x+b与△ABC相离,求b的取值范围;
(2)设直线y=![]() x+3、直线y=﹣
x+3、直线y=﹣![]() x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
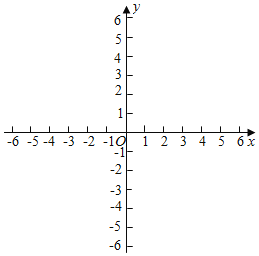
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com