
【题目】小宜跟几位同学在某快餐厅吃饭,如图为此快餐厅的菜单.若他们所点的餐食总共为10份盖饭,x杯饮料,y份凉拌菜.
(1)他们点了 份A套餐, 份B套餐, 份C套餐(均用含x或y的代数式表示);
(2)若x=6,且A、B、C套餐均至少点了1份,则最多有 种点餐方案.

【答案】(1)(10﹣y),(10﹣x),(x+y﹣10);(2)5
【解析】
(1)由三种套餐包含的东西,可用含x或y的代数式表示出他们点了三种套餐的份数;
(2)由x=6及A、B、C套餐均至少点了1份,即可得出关于y的一元一次不等式组,解之即可得出y的取值范围,再结合y为整数即可得出结论.
解:(1)∵B,C套餐都包含一份盖饭和一份凉拌菜,
∴他们点了(10﹣y)份A套餐;
∵A,C套餐都包含一份盖饭和一杯饮料,
∴他们点了(10﹣x)份B套餐;
∴他们点了10﹣(10﹣y)﹣(10﹣x)=(x+y﹣10)份C套餐.
故答案为:(10﹣y);(10﹣x);(x+y﹣10).
(2)依题意,得:![]() ,
,
解得:5≤y≤9.
又∵y为整数,
∴y=5,6,7,8,9,
∴最多有5种点餐方案.
故答案为:5.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与y轴交于点A,与抛物线
的图象与y轴交于点A,与抛物线![]() 的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
(1)求出抛物线的对称轴和点C坐标;
(2)①当![]() 时,直接写出抛物线
时,直接写出抛物线![]() 与图形G的公共点个数.
与图形G的公共点个数.
②如果抛物线![]() 与图形G有且只有一个公共点,求出a的取值范围.
与图形G有且只有一个公共点,求出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
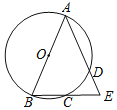
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小志从甲、乙两超市分别购买了10瓶和6瓶cc饮料,共花费51元;小云从甲、乙两超市分别购买了8瓶和12瓶cc饮料,且小云在乙超市比在甲超市多花18元,在小志和小云购买cc饮料时,甲、乙两超市cc饮料价格不一样,若只考虑价格因素,到哪家超市购买这种cc饮料便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
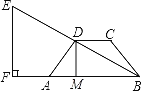
【题目】如图,在四边形ABCD中,AB∥DC,AD=BC,AB=10,CD=4,DM⊥AB于点M.连接BD并延长到E,使DE=BD,作EF⊥AB,交BA的延长线于点F.
(1)求MB的长;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象经过点A(0,﹣4)和B(﹣2,2).
(1)求c的值,并用含a的式子表示b;
(2)当﹣2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
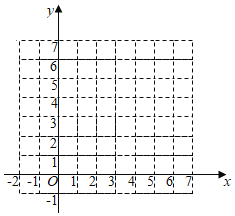
【题目】在平面直角坐标系xOy中,直线x=3与直线y=![]() x+1交于点A,函数y=
x+1交于点A,函数y=![]() (k>0,x>0)的图象与直线x=3,直线y=
(k>0,x>0)的图象与直线x=3,直线y=![]() x+1分别交于点B,C.
x+1分别交于点B,C.
(1)求点A的坐标.
(2)横、纵坐标都是整数的点叫做整点.记函数y=![]() (k>0,x>0)的图象在点B,C之间的部分与线段AB,AC围成的区域(不含边界)为W.
(k>0,x>0)的图象在点B,C之间的部分与线段AB,AC围成的区域(不含边界)为W.
①当k=1时,结合函数图象,求区域W内整点的个数;
②若区域W内恰有1个整点,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
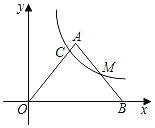
【题目】如图,在平面直角坐标系中,△OAB的边OB在x轴的正半轴上,AO=AB,M是边AB的中点,经过点M的反比例函数y=![]() (k>0,x>0)的图象与边OA交于点C,则
(k>0,x>0)的图象与边OA交于点C,则![]() 的值为__.
的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,对角线AC、BD相交于点O,E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F,连接AF,CE,下列四个结论中:
①对于动点E,四边形AECF始终是平行四边形;
②若∠ABC<90°,则至少存在一个点E,使得四边形AECF是矩形;
③若AB>AD,则至少存在一个点E,使得四边形AECF是菱形;
④若∠BAC=45°,则至少存在一个点E,使得四边形AECF是正方形.
以上所有正确说法的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com