【题目】小志从甲、乙两超市分别购买了10瓶和6瓶cc饮料，共花费51元；小云从甲、乙两超市分别购买了8瓶和12瓶cc饮料，且小云在乙超市比在甲超市多花18元，在小志和小云购买cc饮料时，甲、乙两超市cc饮料价格不一样，若只考虑价格因素，到哪家超市购买这种cc饮料便宜？请说明理由．
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，橫、纵坐标都是整数的点叫做整点．直线y＝ax与抛物线y＝ax2﹣2ax﹣1（a≠0）围成的封闭区域（不包含边界）为W．
（1）求抛物线顶点坐标（用含a的式子表示）；
（2）当a＝
时，写出区域W内的所有整点坐标；
（3）若区域W内有3个整点，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图将一张矩形纸片ABCD沿对角线BD翻折，点C的对应点为C′，AD与BC′交于点E，若∠ABE＝30°，BC＝3，则DE的长度为_____．
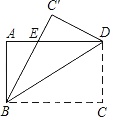
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小石设计的“过直线上一点作这条直线的垂线”的尺规作图过程．
已知：如图1，直线l及直线l上一点P．
求作：直线PQ，使得PQ⊥l．
作法：如图2：
①以点P为圆心，任意长为半径作弧，交直线l于点A，B；
②分别以点A，B为圆心，以大于
AB的同样长为半径作弧，两弧在直线l上方交于点Q；
③作直线PQ．
所以直线PQ就是所求作的直线．
根据小石设计的尺规作图过程：
（1）使用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接QA，QB．
∵QA＝ ，PA＝ ，
∴PQ⊥l （ ）（填推理的依据）．
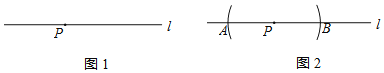
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点E是正方形ABCD内一动点，满足∠AEB＝90°且∠BAE＜45°，过点D作DF⊥BE交BE的延长线于点F．
（1）依题意补全图形；
（2）用等式表示线段EF，DF，BE之间的数量关系，并证明；
（3）连接CE，若AB＝2
，请直接写出线段CE长度的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，∠QAN为锐角，H、B分别为射线AN上的点，点H关于射线AQ的对称点为C，连接AC，CB．
（1）依题意补全图；
（2）CB的垂直平分线交AQ于点E，交BC于点F．连接CE，HE，EB．
①求证：△EHB是等腰三角形；
②若AC+AB＝
AE，求
的值．
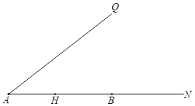
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小宜跟几位同学在某快餐厅吃饭，如图为此快餐厅的菜单．若他们所点的餐食总共为10份盖饭，x杯饮料，y份凉拌菜．
（1）他们点了 份A套餐， 份B套餐， 份C套餐（均用含x或y的代数式表示）；
（2）若x＝6，且A、B、C套餐均至少点了1份，则最多有 种点餐方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A，B是⊙C上的两个点，点P在⊙C的内部．若∠APB为直角，则称∠APB为AB关于⊙C的内直角，特别地，当圆心C在∠APB边（含顶点）上时，称∠APB为AB关于⊙C的最佳内直角．如图1，∠AMB是AB关于⊙C的内直角，∠ANB是AB关于⊙C的最佳内直角．在平面直角坐标系xOy中．
（1）如图2，⊙O的半径为5，A（0，﹣5），B（4，3）是⊙O上两点．
①已知P1（1，0），P2（0，3），P3（﹣2，1），在∠AP1B，∠AP2B，∠AP3B，中，是AB关于⊙O的内直角的是 ；
②若在直线y=2x+b上存在一点P，使得∠APB是AB关于⊙O的内直角，求b的取值范围．
（2）点E是以T（t，0）为圆心，4为半径的圆上一个动点，⊙T与x轴交于点D（点D在点T的右边）．现有点M（1，0），N（0，n），对于线段MN上每一点H，都存在点T，使∠DHE是DE关于⊙T的最佳内直角，请直接写出n的最大值，以及n取得最大值时t的取值范围．
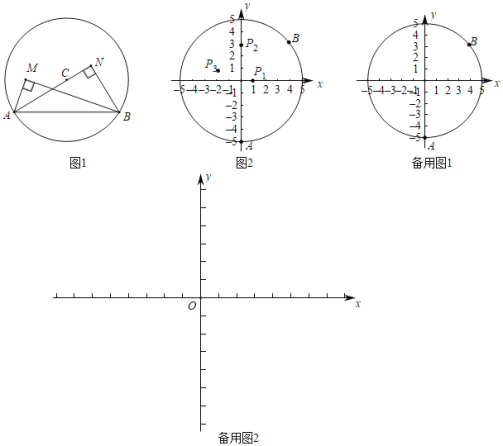
查看答案和解析>>
科目：初中数学 来源： 题型：
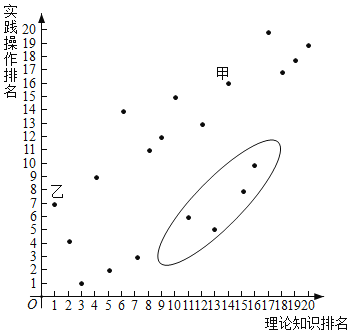
【题目】某公司计划招募10名技术人员，他们对20名面试合格人员进行了测试，测试包括理论知识和实践操作两部分，20名应聘者的成绩排名情况如图所示，下面有3个推断：
①甲测试成绩非常优秀，入选的可能性很大；
②乙的理论知识排名比实践操作排名靠前；
③位于椭圆形区域内的应聘者应该加强该专业理论知识的学习；
其中合理的是_____．（写序号）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
