
【题目】残缺的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.测得AB=24cm,CD=8cm.求这个圆的半径. 
【答案】解:设这个圆的圆心是O,
连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2 ,
解得:x=13.
答:圆的半径为13cm.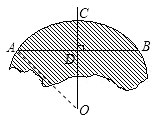
【解析】设这个圆的圆心是O,连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,根据勾股定理可得x2=122+(x﹣8)2 , 解之即可.
【考点精析】本题主要考查了线段垂直平分线的性质和垂径定理的推论的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,反比例函数y= ![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 ![]() ,1),射线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求k和a的值;
(2)直线AC的解析式;
(3)如图3,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的面积为20,点E,F,G为对角线AC的四等分点,连接BE并延长交AD于H,连接HF并延长交BC于点M,则![]() 的面积为
的面积为![]()
![]()
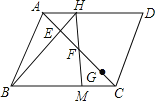
A. 10 B. ![]() C. 4 D. 5
C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下题:
计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).
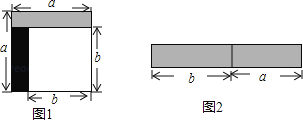
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上. 
(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?答: .
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
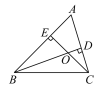
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com