
分析 由于1<$\sqrt{2}$<2,由此可得$\sqrt{2}$的整数部分为1,小数部分m=$\sqrt{2}$-1,然后代入代数式求值.
解答 解:(1)m2+2m
=$(\sqrt{2}-1)^{2}+2(\sqrt{2}-1)$
=1+$2-2\sqrt{2}+1+2\sqrt{2}-2$
=2.
(2)$\sqrt{(m-\frac{1}{m})^{2}}$
=$\sqrt{(\sqrt{2}-1-\frac{1}{\sqrt{2}-1})^{2}}$
=$\sqrt{(\sqrt{2}-1-\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)})^{2}}$
=$\sqrt{(\sqrt{2}-1-\sqrt{2}-1)^{2}}$
=$\sqrt{(-1)^{2}}$
=$\sqrt{1}$
=1.
点评 本题考查了实数的运算和估算无理数的大小,解决本题的关键正确估算无理数的大小.


科目:初中数学 来源: 题型:解答题
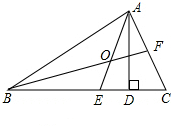 已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
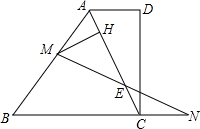 如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.
如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com