
【题目】在平面直角坐标系中,![]() ,
,![]() 且满足:
且满足:![]() ,长方形
,长方形![]() 在坐标系中(如图1),点
在坐标系中(如图1),点![]() 为坐标系的原点.
为坐标系的原点.

(1)求点![]() 的坐标.
的坐标.
(2)如图2,若点![]() 从点
从点![]() 出发,以2个单位/秒的速度向右运动(不超过点
出发,以2个单位/秒的速度向右运动(不超过点![]() ),点
),点![]() 从原点
从原点![]() 出发,以1个单位/秒的速度向下运动(不超过点
出发,以1个单位/秒的速度向下运动(不超过点![]() ),设
),设![]() 两点同时出发,在它们运动的过程中,四边形
两点同时出发,在它们运动的过程中,四边形![]() 的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
科目:初中数学 来源: 题型:
【题目】为了解某校八年级学生参加体育锻炼的情况,随机调查了该校部分学生每周参加体育锻炼的时间,并进行了统计,绘制成图1和图2两幅尚不完整的统计图.

(1)本次共调查学生 人;
(2)这组数据的众数是 ;
(3)请你将图2的统计图补充完整;
(4)若该校八年级共有650人,请根据样本数据,估计每周参加体育锻炼时间为6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
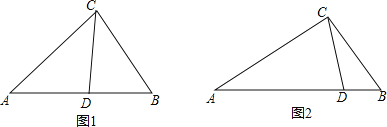
【题目】从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
![]() 如图1,在
如图1,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() ,求证:CD为
,求证:CD为![]() 的完美分割线.
的完美分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 为等腰三角形,求
为等腰三角形,求![]() 的度数.
的度数.
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 是以CD为底边的等腰三角形,求完美分割线CD的长.
是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=5:2,则∠AOF等于( )

A. 140° B. 130° C. 120° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
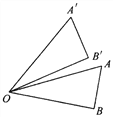
【题目】如图,Rt△AOB绕着一点旋转到△A′OB′的位置,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段和角.已知∠AOB=30°,∠AOB′=10°,那么点B的对应点是点______;线段OB的对应线段是线段_____;∠A的对应角是______;旋转中心是点_______;旋转的角度是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
(1)猜想:∠B的度数,并证明你的猜想.
(2)如果AC=3cm,CD=2cm,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
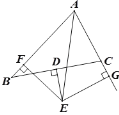
【题目】如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC 的平分线AE于E,EF⊥AB于F,EG⊥AC交AC延长线于G. AB=6, AC=3,求BF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节小明妈妈包了4个蛋黄棕子,6个八宝棕子,10个红枣棕子,从外观上看,它们都一样,
(1)小明吃一个就能吃到黄棕子的概率是多少?
(2)如果爸爸、妈妈每人吃了3个粽子,都没有吃到蛋黄粽子,之后,小明吃一个就吃到蛋黄粽子的概率是多少?如果小明第一个真的吃到了一个蛋黄粽子,那么他再吃一个依然吃到蛋黄粽子的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com