
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)当
;(3)当![]() 时,方式一花费少,理由见解析.
时,方式一花费少,理由见解析.
【解析】
(1)根据两种收费方式分别列出等式计算即可;
(2)根据收费方式,方式一分![]() 和
和![]() 两部分,方式二利用“收费
两部分,方式二利用“收费![]() 单次费用
单次费用![]() 次数”即可得;
次数”即可得;
(3)结合题(2)的结论可得当![]() 时,
时,![]() 关于x的函数表达式,再利用一次函数的性质求解即可得.
关于x的函数表达式,再利用一次函数的性质求解即可得.
(1)当![]() 时,方式二收费为
时,方式二收费为![]() (元)
(元)
当![]() 时,方式一收费为
时,方式一收费为![]() (元)
(元)
当![]() 时,方式二收费为
时,方式二收费为![]() (元)
(元)
故答案为:100,250,400;
(2)由题意,当![]() 时,
时,![]()
当![]() 时,
时,![]()
即![]()
当![]() 时,
时,![]()
故![]() 关于x的函数关系式为
关于x的函数关系式为![]() ,
,![]() 关于x的函数关系式为
关于x的函数关系式为![]() ;
;
(3)方式一花费少,理由如下:
由(2)可知,当![]() 时,
时,![]() ,
,![]()
则![]()
记![]()
因为![]()
所以![]() 随
随![]() 的增大而减小
的增大而减小
又![]() 时,
时,![]() ,即
,即![]()
因此,当![]() 时,
时,![]()
故当![]() 时,方式一花费少.
时,方式一花费少.


科目:初中数学 来源: 题型:
【题目】已知,如图1,在![]() 中,对角线
中,对角线![]() ,
,![]() ,
,![]() ,如图2,点
,如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;将
;将![]() 沿对角线
沿对角线![]() 剪开,
剪开,![]() 从图1的位置与点
从图1的位置与点![]() 同时出发,沿射线
同时出发,沿射线![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,当点
,当点![]() 停止运动时,
停止运动时,![]() 也停止运动.设运动时间为
也停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
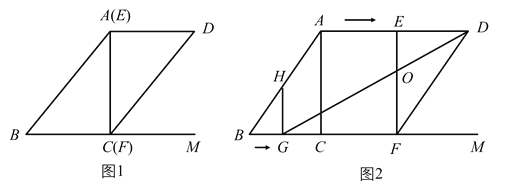
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设四边形![]() 的面积为
的面积为![]() ,试确定
,试确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 有最大值?
有最大值?
(4)连接![]() ,试求当
,试求当![]() 平分
平分![]() 时,四边形
时,四边形![]() 与四边形
与四边形![]() 面积之比.
面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC为弦,点D为![]() 中点,过点D作DE⊥直线AC,垂足为E,交AB的延长线于点F
中点,过点D作DE⊥直线AC,垂足为E,交AB的延长线于点F
(1)求证:EF是⊙O的切线;
(2)若EF=4,sin∠F=![]() ,求⊙O的半径.
,求⊙O的半径.
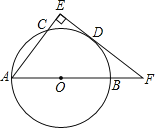
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了调查同学们对学生会的满意度,随机抽取了部分同学作问卷调查:用“![]() ”表示“相 当满意”,“
”表示“相 当满意”,“![]() ”表示“满意”,“
”表示“满意”,“![]() ”表示“比较满意”,“
”表示“比较满意”,“![]() ”表示“不满意”,下图是负责 调查同学根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
”表示“不满意”,下图是负责 调查同学根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人;
(2)通过计算补全条形图;
(3)如果该学校有![]() 名学生,请你估计该校学生对学生会感到“相当满意”的约有多少人?
名学生,请你估计该校学生对学生会感到“相当满意”的约有多少人?
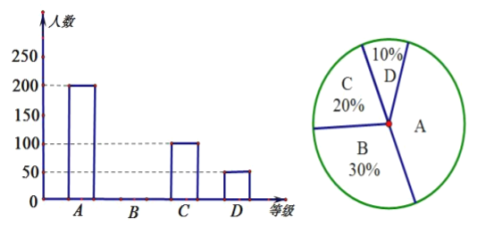
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 点
点![]() 点
点![]()
![]() 是边
是边![]() 上的一点(点
上的一点(点![]() 不与点
不与点![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
(1)如图①,当点![]() 落在边
落在边![]() 上时,求点
上时,求点![]() 的坐标;
的坐标;

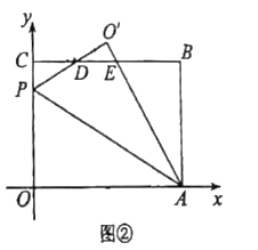
(2)若点![]() 落在边
落在边![]() 的上方,
的上方,![]() 与分别与边
与分别与边![]() 交于点
交于点![]() .
.
①如图②,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
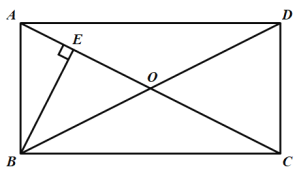
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
(1)求证:![]() ABCD是矩形;
ABCD是矩形;
(2)若AD=![]() ,cos∠ABE=
,cos∠ABE=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础.以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分.
年份 人数 地区 | 2017 | 2018 | 2019 |
东部 | 300 | 147 | 47 |
中部 | 1112 | 181 | |
西部 | 1634 | 916 | 323 |
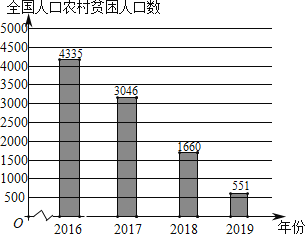
(以上数据来源于国家统计局)
根据统计图表提供的信息,下面推断不正确的是( )
A.2018年中部地区农村贫困人口为597万人
B.2017﹣2019年,农村贫困人口数量都是东部最少
C.2016﹣2019年,农村贫困人口减少数量逐年增多
D.2017﹣2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com