
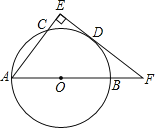
【题目】如图,AB为⊙O的直径,AC为弦,点D为![]() 中点,过点D作DE⊥直线AC,垂足为E,交AB的延长线于点F
中点,过点D作DE⊥直线AC,垂足为E,交AB的延长线于点F
(1)求证:EF是⊙O的切线;
(2)若EF=4,sin∠F=![]() ,求⊙O的半径.
,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
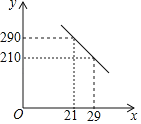
【题目】一名大学毕业生响应国家“自主创业”的号召,在成都市高新区租用了一个门店,聘请了两名员工,计划销售一种产品.已知该产品成本价是20元/件,其销售价不低于成本价,且不高于30元/件,员工每人每天的工资为200元.经过市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)求每件产品销售价为多少元时,每天门店的纯利润最大?最大纯利润是多少?(纯利润=销售收入﹣产品成本﹣员工工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).
用户分类 | 人数 |
A:早期体验用户(目前已升级为5G用户) | 260人 |
B:中期跟随用户(一年内将升级为5G用户) | 540人 |
C:后期用户(一年后才升级为5G用户) | 200人 |
下列推断中,不合理的是( )

A.早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减
B.后期用户中,愿意为5G套餐多支付20元的人数最多
C.愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多
D.愿意为5G套餐多支付20元的用户中,后期用户人数最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠ACB=90°,AC=BC=![]() ,M为BC边上的一个动点(不与点B,C重合),连接AM,以点A为中心,将线段AM逆时针旋转135°,得到线段AN,连接BN.
,M为BC边上的一个动点(不与点B,C重合),连接AM,以点A为中心,将线段AM逆时针旋转135°,得到线段AN,连接BN.

(1)依题意补全图2;
(2)求证:∠BAN=∠AMB;
(3)点P在线段BC的延长线上,点M关于点P的对称点为Q,写出一个PC的值,使得对于任意的点M,总有AQ=BN,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() ,
,![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
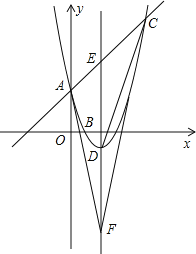
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com