
ЁОЬтФПЁПвЛУћДѓбЇБЯвЕЩњЯьгІЙњМвЁАзджїДДвЕЁБЕФКХейЃЌдкГЩЖМЪаИпаТЧјзтгУСЫвЛИіУХЕъЃЌЦИЧыСЫСНУћдБЙЄЃЌМЦЛЎЯњЪлвЛжжВњЦЗЃЎвбжЊИУВњЦЗГЩБОМлЪЧ20дЊ/МўЃЌЦфЯњЪлМлВЛЕЭгкГЩБОМлЃЌЧвВЛИпгк30дЊ/МўЃЌдБЙЄУПШЫУПЬьЕФЙЄзЪЮЊ200дЊЃЎОЙ§ЪаГЁЕїВщЗЂЯжЃЌИУВњЦЗУПЬьЕФЯњЪлСПyЃЈМўЃЉгыЯњЪлМлxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓУПМўВњЦЗЯњЪлМлЮЊЖрЩйдЊЪБЃЌУПЬьУХЕъЕФДПРћШѓзюДѓЃПзюДѓДПРћШѓЪЧЖрЩйЃПЃЈДПРћШѓЃНЯњЪлЪеШыЉВњЦЗГЩБОЉдБЙЄЙЄзЪЃЉ
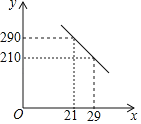
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ10x+500ЃЈ20ЁмxЁм30ЃЉЃЛЃЈ2ЃЉЕБxЃН30ЪБЃЌУПЬьУХЕъЕФДПРћШѓWзюДѓЃЌзюДѓЮЊ1600дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИљОнДПРћШѓЃНЯњЪлЪеШыЉВњЦЗГЩБОЉдБЙЄЙЄзЪСаГіЖўДЮКЏЪ§НтЮіЪНЃЌИљОнЖўДЮКЏЪ§ЕФаджЪНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉЩшyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊyЃНkx+bЃЌ
АбЃЈ21ЃЌ290ЃЉЁЂЃЈ29ЃЌ210ЃЉДњШыЃЌ
ЕУ![]() ЃЌ
ЃЌ
НтЕУЃЌ![]() ЃЌ
ЃЌ
дђyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊyЃНЉ10x+500ЃЈ20ЁмxЁм30ЃЉЃЛ
ЃЈ2ЃЉУПЬьУХЕъЕФДПРћШѓWЃНЃЈЉ10x+500ЃЉЃЈxЉ20ЃЉЉ400
ЃНЉ10x2+700xЉ10400
ЃНЉ10ЃЈxЉ35ЃЉ2+1850ЃЌ
Ёп20ЁмxЁм30ЃЌ
ЁрЕБxЃН30ЪБЃЌУПЬьУХЕъЕФДПРћШѓWзюДѓЃЌзюДѓЮЊ1600дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌМЧКЏЪ§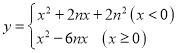 ЕФЭМЯѓЮЊ
ЕФЭМЯѓЮЊ![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЕФЖдГЦжааФгыдЕужиКЯЃЌЖЅЕу
ЕФЖдГЦжааФгыдЕужиКЯЃЌЖЅЕу![]() ЕФзјБъЮЊЃЈ2,2ЃЉЃЌЕу
ЕФзјБъЮЊЃЈ2,2ЃЉЃЌЕу![]() дкЕкЫФЯѓЯоЃЎ
дкЕкЫФЯѓЯоЃЎ
ЃЈ1ЃЉЕБ![]() ЃН1ЪБЃЎ
ЃН1ЪБЃЎ
ЂйЧѓ![]() ЕФзюЕЭЕуЕФзнзјБъЃЛ
ЕФзюЕЭЕуЕФзнзјБъЃЛ
ЂкЧѓЭМЯѓ![]() ЩЯЫљгаЕН
ЩЯЫљгаЕН![]() жсЕФОрРыЮЊ2ЕФКсзјБъжЎКЭЃЎ
жсЕФОрРыЮЊ2ЕФКсзјБъжЎКЭЃЎ
ЂлШєЕБ![]() Ём
Ём![]() Ём
Ём![]() ЪБЃЌЃ9Ём
ЪБЃЌЃ9Ём![]() Ём2ЃЌдђ
Ём2ЃЌдђ![]() ЁЂ
ЁЂ![]() ЕФЖдгІжЕЮЊ ЃЎ
ЕФЖдгІжЕЮЊ ЃЎ
ЃЈ2ЃЉЕБЭМЯѓ![]() гые§ЗНаЮ
гые§ЗНаЮ![]() ЕФБпЧЁКУгаСНИіЙЋЙВЕуЪБЃЌжБНгаДГі
ЕФБпЧЁКУгаСНИіЙЋЙВЕуЪБЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМ1ЃЌдк![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШчЭМ2ЃЌЕу
ЃЌШчЭМ2ЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ
ЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЛНЋ
ЃЛНЋ![]() биЖдНЧЯп
биЖдНЧЯп![]() МєПЊЃЌ
МєПЊЃЌ![]() ДгЭМ1ЕФЮЛжУгыЕу
ДгЭМ1ЕФЮЛжУгыЕу![]() ЭЌЪБГіЗЂЃЌбиЩфЯп
ЭЌЪБГіЗЂЃЌбиЩфЯп![]() ЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ
ЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ЭЃжЙдЫЖЏЪБЃЌ
ЭЃжЙдЫЖЏЪБЃЌ![]() вВЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊ
вВЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊ![]() ЃЌНтД№ЯТСаЮЪЬтЃК
ЃЌНтД№ЯТСаЮЪЬтЃК
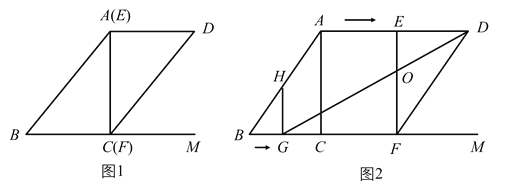
ЃЈ1ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЕу
ЮЊКЮжЕЪБЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФДЙжБЦНЗжЯпЩЯЃП
ЕФДЙжБЦНЗжЯпЩЯЃП
ЃЈ2ЃЉЩшЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЪдШЗЖЈ
ЃЌЪдШЗЖЈ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() газюДѓжЕЃП
газюДѓжЕЃП
ЃЈ4ЃЉСЌНг![]() ЃЌЪдЧѓЕБ
ЃЌЪдЧѓЕБ![]() ЦНЗж
ЦНЗж![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() гыЫФБпаЮ
гыЫФБпаЮ![]() УцЛ§жЎБШЃЎ
УцЛ§жЎБШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН6ЃЌBCЃН8ЃЌЕуEЪЧBCБпЩЯвЛЕуЃЌСЌНгAEЃЌАбЁЯBбиAEелЕўЃЌЪЙЕуBТфдкЕуBЁфДІЃЌЕБЁїCEBЁфЮЊжБНЧШ§НЧаЮЪБЃЌBEЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+cЕФЭМЯѓШчЭМЫљЪОЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
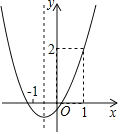
A.abcЃО0B.aЉb+cЃН2
C.4acЉb2ЃМ0D.ЕБxЃОЉ1ЪБЃЌyЫцxдіДѓЖјдіДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
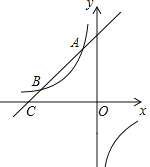
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНx+bЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЃЈkЮЊГЃЪ§ЧвkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈЉ1ЃЌaЃЉЁЂBСНЕуЃЌгыxжсНЛгкЕуCЃЈЉ4ЃЌ0ЃЉЃЎ
ЃЈkЮЊГЃЪ§ЧвkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈЉ1ЃЌaЃЉЁЂBСНЕуЃЌгыxжсНЛгкЕуCЃЈЉ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєЕуDЪЧЕкЫФЯѓЯоФкЗДБШР§КЏЪ§ЭМЯѓЩЯЕФЕуЃЌЧвЕуDЕНжБЯпACЕФОрРыЮЊ5![]() ЃЌЧѓЕуDЕФКсзјБъЃЎ
ЃЌЧѓЕуDЕФКсзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
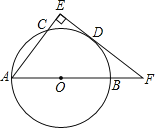
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌACЮЊЯвЃЌЕуDЮЊ![]() жаЕуЃЌЙ§ЕуDзїDEЁЭжБЯпACЃЌДЙзуЮЊEЃЌНЛABЕФбгГЄЯпгкЕуF
жаЕуЃЌЙ§ЕуDзїDEЁЭжБЯпACЃЌДЙзуЮЊEЃЌНЛABЕФбгГЄЯпгкЕуF
ЃЈ1ЃЉЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєEFЃН4ЃЌsinЁЯFЃН![]() ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=1ЃЌAD=2ЃЌЕуEЪЧБпADЩЯЕФвЛИіЖЏЕуЃЌАбЁїBAEбиBEелЕўЃЌЕуAТфдкAЁфДІЃЌШчЙћAЁфЧЁдкОиаЮЕФЖдГЦжсЩЯЃЌдђAEЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
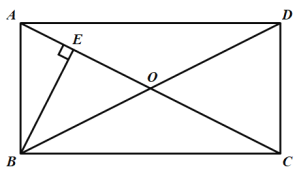
ЁОЬтФПЁПШчЭМЃЌдк![]() ABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌOA=OBЃЌЙ§ЕуBзїBEЁЭACгкЕуEЃЎ
ABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌOA=OBЃЌЙ§ЕуBзїBEЁЭACгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ABCDЪЧОиаЮЃЛ
ABCDЪЧОиаЮЃЛ
ЃЈ2ЃЉШєAD=![]() ЃЌcosЁЯABE=
ЃЌcosЁЯABE=![]() ЃЌЧѓACЕФГЄЃЎ
ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com