
【题目】在平面直角坐标系中,记函数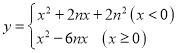 的图象为
的图象为![]() ,正方形
,正方形![]() 的对称中心与原点重合,顶点
的对称中心与原点重合,顶点![]() 的坐标为(2,2),点
的坐标为(2,2),点![]() 在第四象限.
在第四象限.
(1)当![]() =1时.
=1时.
①求![]() 的最低点的纵坐标;
的最低点的纵坐标;
②求图象![]() 上所有到
上所有到![]() 轴的距离为2的横坐标之和.
轴的距离为2的横坐标之和.
③若当![]() ≤
≤![]() ≤
≤![]() 时,-9≤
时,-9≤![]() ≤2,则
≤2,则![]() 、
、![]() 的对应值为 .
的对应值为 .
(2)当图象![]() 与正方形
与正方形![]() 的边恰好有两个公共点时,直接写出
的边恰好有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①-9;②![]() ;③a=-2,b=
;③a=-2,b=![]() ;(2)当
;(2)当![]() 或
或![]() 或
或![]() 时图象G与正方形ABCD的边恰好有两个公共点
时图象G与正方形ABCD的边恰好有两个公共点
【解析】
(1)①将n=1分别代入两个函数解析式,分别求出其顶点坐标即可得出结论;
②分别求出两函数值为2时对应的x的值,再求和即可;
③分别求出y=-9,y=2时对应的x的值,即可确定a,b的值;
(2)分三种情况讨论,由图象G与正方形ABCD的边恰好有两个公共点,列出不等式,可求解.
(1)①把![]() 代入
代入![]() 得,
得,![]() ,
,
![]() ,
,
∴其顶点坐标为![]() ;
;
把![]() 代入
代入![]() (x≥0)得,
(x≥0)得,![]()
![]()
∴其顶点坐标为(3,-9),
∵a>0,
∴函数![]() 和函数
和函数![]() 的图象均开口向上,
的图象均开口向上,
∴图象G有最低点,最低点的纵坐标为:-9;
②对于![]() ,当y=2时,
,当y=2时,![]() ,
,
解得,![]() ,
,![]()
![]()
![]()
对于![]() ,当y=2时,
,当y=2时,![]()
解得,![]() ,
,![]()
![]()
![]()
∴图象![]() 上所有到
上所有到![]() 轴的距离为2的横坐标之和为:
轴的距离为2的横坐标之和为:![]() ;
;
③当y=-9时,即![]() ,解得x1=x2=3;
,解得x1=x2=3;
当y=2时,![]() ,
,![]()
∴当-9≤![]() ≤2时,-2≤x≤
≤2时,-2≤x≤![]() ,
,
又![]() ≤
≤![]() ≤
≤![]()
∴a=-2,b=![]()
(2)对于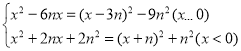
若![]() 的顶点在正方形ABCD内部时,
的顶点在正方形ABCD内部时,
![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,
此时![]() 与正方形ABCD的边也有一个交点,
与正方形ABCD的边也有一个交点,
![]() 符合题意;
符合题意;
若![]() 的顶点不在正方形ABCD的内部时,且与正方形的边有一个交点,
的顶点不在正方形ABCD的内部时,且与正方形的边有一个交点,
![]() ,
,
![]()
即![]() 与正方形ABCD的边有一个交点,
与正方形ABCD的边有一个交点,
![]()
![]()
![]() ;
;
若![]() 的顶点在正方形ABCD的边上时,图象G与正方形ABCD的边恰好有两个公共点,
的顶点在正方形ABCD的边上时,图象G与正方形ABCD的边恰好有两个公共点,
![]() ,
,
![]() ,
,
综上所述,当![]() 或
或![]() 或
或![]() 时图象G与正方形ABCD的边恰好有两个公共点.
时图象G与正方形ABCD的边恰好有两个公共点.


科目:初中数学 来源: 题型:
【题目】在建设港珠澳大桥期间,大桥的规划选线须经过中华白海豚国家级白然保护区—区域![]() 或区域
或区域![]() .为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海
.为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海![]() 天,在区域
天,在区域![]() 、
、![]() 两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
(收集数据)
连续![]() 天观察中华白海豚每天在区域
天观察中华白海豚每天在区域![]() 、区域
、区域![]() 出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(整理、描述数据)
(1)按如下数段整理、描述这两组数据,请补充完整:
海豚数 |
|
|
|
|
|
区域 |
|
|
| _________ | _________ |
区域 |
|
|
|
|
|
(2)两组数据的平均数、中位数,众数如下所示:
观测点 | 平均数 | 中位数 | 众数 |
区域 |
|
|
|
区域 |
|
|
|
请填空:上表中中位数![]() _______,,众数
_______,,众数![]() ______;
______;
(3)规划者们选择了区域![]() 为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的
为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的![]() 天施工期内,区域
天施工期内,区域![]() 大约有多少天中华白海豚出现的数目在
大约有多少天中华白海豚出现的数目在![]() 的范围内?
的范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2mx+m2+m-1(m是常数).
(1)求证:不论m为何值,该函数的图像的顶点都在函数y=x-1的图像上.
(2)若该函数的图像与函数y=x+b的图像有两个交点,则b的取值范围为( )
A.b>0 B.b>-1 C.b>-![]() D.b>-2
D.b>-2
(3)该函数图像与坐标轴交点的个数随m的值变化而变化,直接写出交点个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
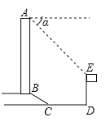
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆![]() ,从办公大楼顶端
,从办公大楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是45°,旗杆底端
是45°,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是10米,梯坎坡长
是10米,梯坎坡长![]() 是10米,梯坎坡度
是10米,梯坎坡度![]() =1:
=1:![]() ,则大楼
,则大楼![]() 的高为______米.
的高为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
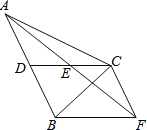
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
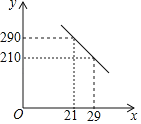
【题目】一名大学毕业生响应国家“自主创业”的号召,在成都市高新区租用了一个门店,聘请了两名员工,计划销售一种产品.已知该产品成本价是20元/件,其销售价不低于成本价,且不高于30元/件,员工每人每天的工资为200元.经过市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)求每件产品销售价为多少元时,每天门店的纯利润最大?最大纯利润是多少?(纯利润=销售收入﹣产品成本﹣员工工资)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com