
【题目】已知,如图1,在![]() 中,对角线
中,对角线![]() ,
,![]() ,
,![]() ,如图2,点
,如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;将
;将![]() 沿对角线
沿对角线![]() 剪开,
剪开,![]() 从图1的位置与点
从图1的位置与点![]() 同时出发,沿射线
同时出发,沿射线![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,当点
,当点![]() 停止运动时,
停止运动时,![]() 也停止运动.设运动时间为
也停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
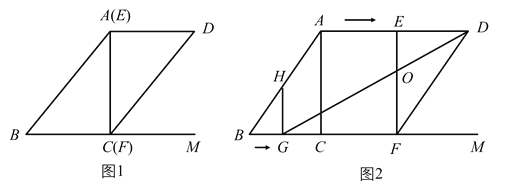
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设四边形![]() 的面积为
的面积为![]() ,试确定
,试确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 有最大值?
有最大值?
(4)连接![]() ,试求当
,试求当![]() 平分
平分![]() 时,四边形
时,四边形![]() 与四边形
与四边形![]() 面积之比.
面积之比.
【答案】(1)![]() ,(2)
,(2)![]() 四边形AHGD
四边形AHGD ![]()
(3)当![]() 四边形
四边形![]() 的面积最大,最大面积为
的面积最大,最大面积为![]()
(4)![]()
【解析】
(1)由题意得:![]() 利用垂直平分线的性质得到:
利用垂直平分线的性质得到:![]() 列方程求解即可,
列方程求解即可,
(2)![]() 四边形AHGD
四边形AHGD![]() 分别求出各图形的面积,代入计算即可得到答案,
分别求出各图形的面积,代入计算即可得到答案,
(3)利用(2)中解析式,结合二次函数的性质求最大面积即可,
(4)连接![]() 过
过![]() 作
作![]() 于
于![]() 从而求解此时时间
从而求解此时时间![]() ,分别求解四边形EGFD和四边形AHGE的面积,即可得到答案.
,分别求解四边形EGFD和四边形AHGE的面积,即可得到答案.
解:(1)如图,由题意得:![]()
![]()
![]()
![]() 及平移的性质,
及平移的性质,
![]()
![]() 点
点![]() 在线段
在线段![]() 的垂直平分线上,
的垂直平分线上,
![]()
![]()
![]()
当![]() 时,点
时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.

(2)![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]() 点在
点在![]() 上,
上,
![]()
![]()
![]()
![]() 四边形AHGD
四边形AHGD![]()
![]() (
(![]() )
)
(3)![]()
![]() 四边形AHGD
四边形AHGD ![]() 且
且![]()
![]() 抛物线的对称轴是:
抛物线的对称轴是:![]()
![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() 四边形
四边形![]() 的面积最大,最大面积为:
的面积最大,最大面积为:
![]()
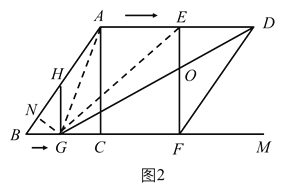
(4)如图,连接![]() 过
过![]() 作
作![]() 于
于![]()
![]() 平分
平分![]()
![]()
![]()
![]()
![]()
![]()
此时:![]()
由![]()
![]()
![]() 四边形EGFD
四边形EGFD![]()
![]() 四边形ABGE
四边形ABGE![]()
![]()
![]() 四边形AHGE
四边形AHGE![]() .
.
![]() 四边形EGFD:
四边形EGFD:![]() 四边形AHGE
四边形AHGE![]()


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2mx+m2+m-1(m是常数).
(1)求证:不论m为何值,该函数的图像的顶点都在函数y=x-1的图像上.
(2)若该函数的图像与函数y=x+b的图像有两个交点,则b的取值范围为( )
A.b>0 B.b>-1 C.b>-![]() D.b>-2
D.b>-2
(3)该函数图像与坐标轴交点的个数随m的值变化而变化,直接写出交点个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
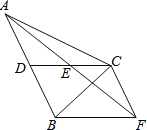
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
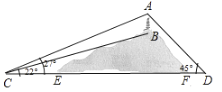
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
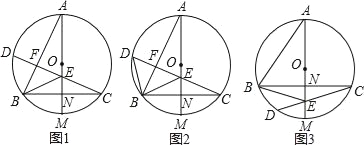
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名大学毕业生响应国家“自主创业”的号召,在成都市高新区租用了一个门店,聘请了两名员工,计划销售一种产品.已知该产品成本价是20元/件,其销售价不低于成本价,且不高于30元/件,员工每人每天的工资为200元.经过市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)求每件产品销售价为多少元时,每天门店的纯利润最大?最大纯利润是多少?(纯利润=销售收入﹣产品成本﹣员工工资)
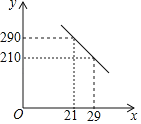
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com