
【题目】已知抛物线y=ax2+bx+c的图象如图所示,下列说法正确的是( )
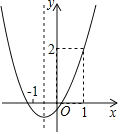
A.abc>0B.a﹣b+c=2
C.4ac﹣b2<0D.当x>﹣1时,y随x增大而增大
【答案】C
【解析】
A、根据抛物线y=ax2+bx+c的图象可得a>0,b>0,c<0,即可判断;B、当x=﹣1时,y<0,即可判断;C、因为抛物线与x轴有两个交点,可得△>0即可判断;D、当x>﹣1时,在对称轴左侧y随x的增大而减小,在对称轴右侧,y随x增大而增大,即可判断.
解:根据抛物线y=ax2+bx+c的图象可知:
A、a>0,b>0,c<0,
∴abc<0,
所以A选项错误;
B、当x=﹣1时,y<0,
即a﹣b+c<0,
所以B选项错误;
C、因为抛物线与x轴有两个交点,
所以△>0,即b2﹣4ac>0,
所以4ac﹣b2<0,
所以C选项正确;
D、当x>﹣1时,在对称轴左侧y随x的增大而减小,在对称轴右侧,y随x增大而增大,
所以D选项错误.
故选:C.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
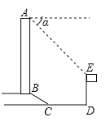
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆![]() ,从办公大楼顶端
,从办公大楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是45°,旗杆底端
是45°,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是10米,梯坎坡长
是10米,梯坎坡长![]() 是10米,梯坎坡度
是10米,梯坎坡度![]() =1:
=1:![]() ,则大楼
,则大楼![]() 的高为______米.
的高为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
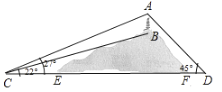
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字40个,比赛结束后随机抽查部分学生听写“正确的字数”,以下是根据抽查结果绘制的统计图表.
频数分布表
组别 | 正确的字数 | 人数 |
| 0.5~8.5 | 10 |
| 8.5~16.5 | 15 |
| 16.5~24.5 | 25 |
| 24.5~32.5 |
|
| 32.5~40.5 |
|
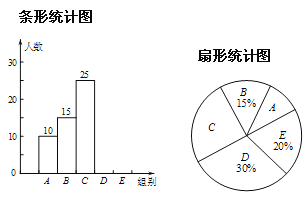
根据以上信息解决下列问题:
(1)补全条形统计图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是_________;
组”所对应的圆心角的度数是_________;
(3)若该校共有1210名学生,如果听写正确的字数少于25,则定为不合格;请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
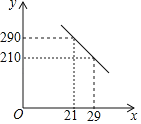
【题目】一名大学毕业生响应国家“自主创业”的号召,在成都市高新区租用了一个门店,聘请了两名员工,计划销售一种产品.已知该产品成本价是20元/件,其销售价不低于成本价,且不高于30元/件,员工每人每天的工资为200元.经过市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)求每件产品销售价为多少元时,每天门店的纯利润最大?最大纯利润是多少?(纯利润=销售收入﹣产品成本﹣员工工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).
用户分类 | 人数 |
A:早期体验用户(目前已升级为5G用户) | 260人 |
B:中期跟随用户(一年内将升级为5G用户) | 540人 |
C:后期用户(一年后才升级为5G用户) | 200人 |
下列推断中,不合理的是( )

A.早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减
B.后期用户中,愿意为5G套餐多支付20元的人数最多
C.愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多
D.愿意为5G套餐多支付20元的用户中,后期用户人数最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() ,
,![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
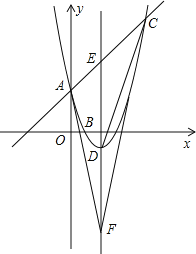
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2+PB2=PC2,则称点P为△ABC关于点C的勾股点.

(1)如图2,在4×3的方格纸中,每个小正方形的边长均为1,△ABC的顶点在格点上,请找出所有的格点P,使点P为△ABC关于点A的勾股点.
(2)如图3,△ABC为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角三角形APD(点A、P、D顺时针排列)∠PAD=90°,连接DC,DB,求证:点P为△BDC关于点D的勾股点.
(3)如图4,点E是矩形ABCD外一点,且点C是△ABE关于点A的勾股点,若AD=8,CE=5,AD=DE,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com