
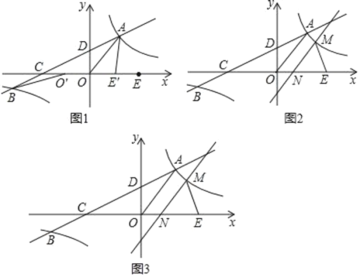
【题目】如图1,在平面直角坐标系xOy中,双曲线![]() 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
(1)将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;
(2)将直线OA沿射线OE平移,平移过程中交![]() 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
【答案】(1)存在,|BO′﹣AE′|的最大值为![]() ,此时点O′的坐标(﹣
,此时点O′的坐标(﹣![]() ,0);(2)存在,M(
,0);(2)存在,M(![]() )或(8,
)或(8,![]() ).
).
【解析】
(1)把A向左平移5个单位得A1(-2,4),作B关于x轴的对称点B1,则有|BO′-AE′|=|BO′-A1O′|=B1O′-A1O′|≤A1B1,想办法求出A1B1,直线A1B1的解析式即可解决问题;
(2)设M(m,![]() ),则N(m
),则N(m![]() ,0),NE2=(5-m+
,0),NE2=(5-m+![]() )2,ME2=(5-m)2+(
)2,ME2=(5-m)2+(![]() )2,MN2=(
)2,MN2=(![]() )2+(
)2+(![]() )2,分MN=EM,MN=NE两种情形,分别构建方程即可解决问题.
)2,分MN=EM,MN=NE两种情形,分别构建方程即可解决问题.
(1)如图1中,
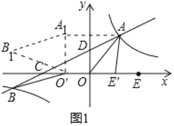
∵A(3,4),
∴OA=![]() =5,
=5,
∵OA=OC=OE,
∴OA=OC=OE=5,
∴C(﹣5,0),E(5,0),
把A、C两点坐标代入y=ax+b得到![]() ,
,
解得![]() ,
,
∴直线的解析式为:![]() ,
,
把A(3,4)代入y=![]() 中,得到k=12,
中,得到k=12,
∴反比例函数的解析式为y=![]() ,
,
把A向左平移5个单位得A1(﹣2,4),作B关于x轴的对称点B1,
则有|BO′﹣AE′|=|BO′﹣A1O′|=|B1O′﹣A1O′|≤A1B1,
直线AC:![]() ,
,
双曲线:![]() ,
,
∴B(﹣8,﹣![]() ),B1(﹣8,
),B1(﹣8,![]() ),
),
∴A1B1=![]() ,
,
直线A1B1:![]() ,
,
令y=0,可得x=﹣![]() ,
,
∴O′(﹣![]() ,0).
,0).
∴|BO′﹣AE′|的最大值为![]() ,此时点O′的坐标(﹣
,此时点O′的坐标(﹣![]() ,0).
,0).
(2)设M(m,![]() ),则N(m﹣
),则N(m﹣![]() ,0),
,0),
∴NE2=(5﹣m+![]() )2,ME2=(5﹣m)2+(
)2,ME2=(5﹣m)2+(![]() )2,MN2=(
)2,MN2=(![]() )2+(
)2+(![]() )2
)2
若MN=ME,则有,(5﹣m)2+(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得:m=![]() 或
或![]() (舍弃),
(舍弃),
∴M(![]() ,
,![]() ),
),
若MN=NE,则有(5﹣m+![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,解得m=8或3(舍弃),
)2,解得m=8或3(舍弃),
∴M(8,![]() ),
),
综上所述,满足条件的点M的坐标为(![]() ,
,![]() )或(8,
)或(8,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同:
甲果园:每人需购买20元的门票一张,采摘的草莓按6折优惠;
乙果园:不需要购买门票,采摘的草莓按售价付款不优惠.
设小明和爸爸妈妈三个人采摘的草莓数量为![]() 千克,在甲、乙果园采摘所需总费用分别为
千克,在甲、乙果园采摘所需总费用分别为![]() 、
、![]() 元,其函数图象如图所示.
元,其函数图象如图所示.

(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请求出图中点![]() 的坐标;
的坐标;
(3)请根据函数图象,直接写出小明一家选择哪家果园采摘更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1的矩形ABCD中,E点在AD上,且AB=![]() ,AE=1.今分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图.若图2中,∠AED=15°,则∠AEC的度数是( )
,AE=1.今分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图.若图2中,∠AED=15°,则∠AEC的度数是( )
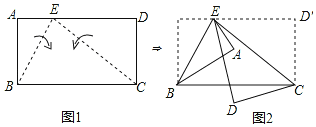
A.10°B.15°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月10日是我国第35个教师节,某中学德育处发起了感恩小学恩师的活动,德育处要求每位同学从以下三种方式中选择一种方式表达感恩:A.信件感恩,B.信息感恩,C.当面感恩.为了解同学们选择以上三种感恩方式的情况,德育处随机对本校部分学生进行了调查,井根据调查结果绘制成了如下两幅不完整的统计图.
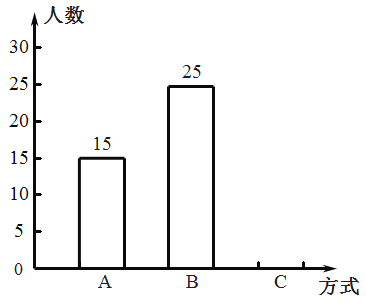
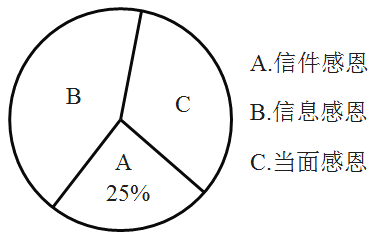
根据图中信息,解答下列问题:
(1)扇形统计图中C部分所对应的扇形圆心角的度数为________,并补全条形统计图;
(2)本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学,德育处打算从他们四个人中选择两位在主题升旗仪式上发言,请用画树状图或列表的方法求恰好选到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,OA=8,AB=6,点D在边BC上,且CD=3DB,点E是边OA上一点,连接DE,将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,则OE的长为_____.
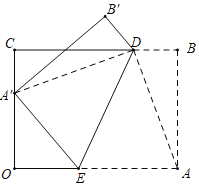
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D在边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,则EF的长度为_____.
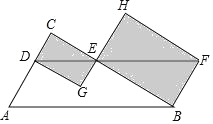
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)在(1)中,△PQB的面积能否等于8cm2?说明理由.
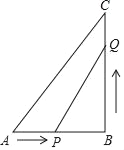
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com