
分析 (1)把x2+y2化为(x+y)2-2xy,代入已知数据计算即可;
(2)把x2y+xy2化为xy(x+y),代入已知数据计算即可;
(3)把x-y化为$\sqrt{({x-y)}^{2}}$,根据完全平方公式计算即可.
解答 解:(1)x2+y2=(x+y)2-2xy=82-2×(-5)=74;
(2)x2y+xy2=xy(x+y)=-5×8=-40;
(3)x-y=$\sqrt{({x-y)}^{2}}$=$\sqrt{(x+y)^{2}-4xy}$=$\sqrt{{8}^{2}-4×(-5)}$=$\sqrt{84}$=2$\sqrt{21}$.
点评 本题考查了完全平方公式的运用,熟练掌握完全平方公式:(a±b)2=a2±2ab+b2是解本题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
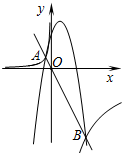 如图,直线y=-2x与抛物线y=-x2+mx+6交于A、B两点,过A、B两点的双曲线的解析式分别为$y=\frac{k_1}{x}$、$y=\frac{k_2}{x}$,则k1k2的值为( )
如图,直线y=-2x与抛物线y=-x2+mx+6交于A、B两点,过A、B两点的双曲线的解析式分别为$y=\frac{k_1}{x}$、$y=\frac{k_2}{x}$,则k1k2的值为( )| A. | -6 | B. | 36 | C. | 72 | D. | 144 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 城市中心立体绿化面积 | B. | PM2.5 | ||
| C. | 雾霾 | D. | 雾霾程度 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
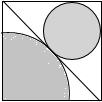 如图,在边长为a的大正方形的对角线一边作一个足够大的小圆,在另一边作一个足够大的四分之一圆,则这两个阴影部分的面积比为(3+2$\sqrt{2}$):4.
如图,在边长为a的大正方形的对角线一边作一个足够大的小圆,在另一边作一个足够大的四分之一圆,则这两个阴影部分的面积比为(3+2$\sqrt{2}$):4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
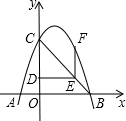 如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com