
【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.4).
=2.4).
【答案】
(1)
解:延长BA交EF于点G,在Rt△AGE中,
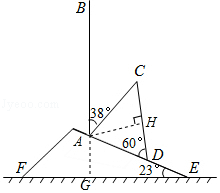
∵∠E=23°,
∴∠GAE=67°.
又∵∠BAC=38°,
∴∠CAE=180°﹣67°﹣38°=75°
(2)
解:过点A作AH⊥CD,垂足为H.
在△ADH中,
∵∠ADC=60°,AD=6m,
∴DH=ADcos∠ADC=6cos60°=3,AH=ADsin∠ADC=6sin60°=3 ![]() .
.
在Rt△ACH中,∠C=180°﹣75°﹣60°=45°,
∴CH=AH=3 ![]() ,
,
∴AC= ![]() =
= ![]() =
= ![]() =3
=3 ![]()
∴AB=AC+CD=3 ![]() +3
+3 ![]() +3≈15(米)
+3≈15(米)

【解析】(1)延长BA交EF于点G,根据直角三角形的性质求出∠GAE的度数,再由补角的定义即可得出结论;(2)过点A作AH⊥CD,垂足为H,在△ADH中,利用锐角三角函数的定义求出DH的长,同理可得出AC的长,由AB=AC+CD即可得出结论.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
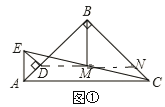
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.
(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为______________;
(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潍坊到济南的距离约为210km,小刘开着小轿车,小张开着大货车,都从潍坊去济南,小刘比小张晚出发1小时,最后两车同时到达济南,已知小轿车的速度是大货车速度的1.5倍.
(1)求小轿车和大货车的速度各是多少?(列方程解答)
(2)当小刘出发时,求小张离济南还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班计划购买篮球和排球若干个,买4个篮球和3个排球需要410元;买2个篮球和5个排球需要310元.
(1)篮球和排球单价各是多少元?
(2)若两种球共买30个,费用不超过1700元,篮球最多可以买多少个?
(3)如果购买这两种球刚好用去520元,问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
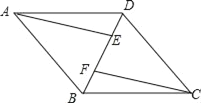
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题: 如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.
小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是 . 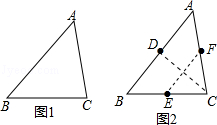
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:
(1)当a=﹣1,b=2时,求代数式﹣2(ab﹣3b2)﹣[6b2﹣(ab﹣a2)]的值
(2)先化简,再求值:4xy﹣2(![]() x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
(3)若(2mx2﹣x+3)﹣(3x2﹣x﹣4)的结果与x的取值无关,求m的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com