
【题目】潍坊到济南的距离约为210km,小刘开着小轿车,小张开着大货车,都从潍坊去济南,小刘比小张晚出发1小时,最后两车同时到达济南,已知小轿车的速度是大货车速度的1.5倍.
(1)求小轿车和大货车的速度各是多少?(列方程解答)
(2)当小刘出发时,求小张离济南还有多远?
【答案】
(1)解:设大货车速度为xkm/h,则小轿车的速度为1.5x km/h,
根据题意得: ![]() ﹣
﹣ ![]() =1,
=1,
解得:x=70,
经检验,x=70是原分式方程的解,
∴1.5x=105
(2)解:210﹣70×1=140(km)
【解析】(1)设大货车速度为xkm/h,则小轿车的速度为1.5x km/h,根据时间=路程÷速度结合二者所需时间之间的关系,即可得出关于x的分式方程,解之并检验后,即可得出结论;(2)根据距离=总距离﹣1小时行驶的路程,即可求出当小刘出发时,小张离济南的距离.
【考点精析】根据题目的已知条件,利用分式方程的应用的相关知识可以得到问题的答案,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图1,两个形状、大小完全相同的含有30゜和60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
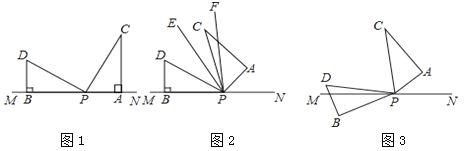
(1)试说明:∠DPC=90゜;
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动),以下两个结论:①![]() 为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2+bx﹣3经过点A(7,﹣3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
(1)求m的值;
(2)求这条抛物线的表达式;
(3)点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
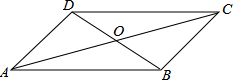
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.4).
=2.4).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发
的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路
以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距
离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
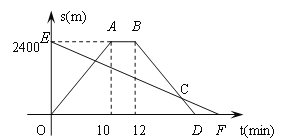
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
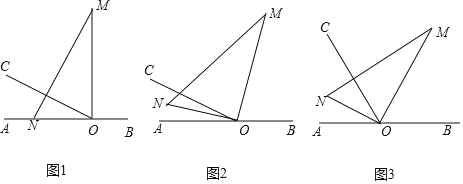
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后OM恰好平分∠BOC,则t= (直接写结果)
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多少秒后OC平分∠MON?请说明理由;
(3)在(2)问的基础上,那么经过多少秒∠MOC=36°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.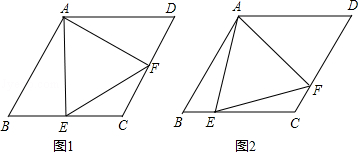
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com