
【题目】(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发
的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路
以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距
离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
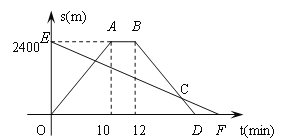
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
【答案】(1)S2=2400-96t(0≤t≤25)
(2)20min追上,距离家还有480m.
【解析】
试题(1)由题意可知小明爸爸以96m/min速度从邮局同一条道路步行2400m回家,所以小明爸爸与
家之间的距离为s2=2400-96t(0≤t≤25);(2)先利用条件求出直线BD的解析式S1=-240t+5280,然后求
S1,s2的交点C的坐标即可.
试题解析:(1)易求S2=2400-96t(0≤t≤25) 3分
(2)小明速度=![]() (m/min),所以小明在回家时的图象BD的解析式为:
(m/min),所以小明在回家时的图象BD的解析式为:
S1=2400-240(t-12)=2400+2880-240t=-240t+5280 5分
将两个函数联立成方程组得:
 6分
6分
解得![]() 8分
8分
答:20min追上,距离家还有480m. 9分


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,绵阳市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: 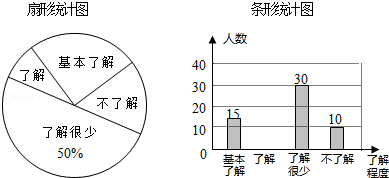
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若该中学共有学生3000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
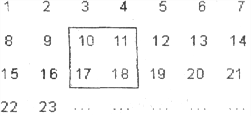
【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潍坊到济南的距离约为210km,小刘开着小轿车,小张开着大货车,都从潍坊去济南,小刘比小张晚出发1小时,最后两车同时到达济南,已知小轿车的速度是大货车速度的1.5倍.
(1)求小轿车和大货车的速度各是多少?(列方程解答)
(2)当小刘出发时,求小张离济南还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
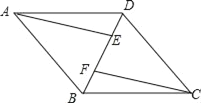
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公租房倍受社会关注,2012年竣工的公租房有A,B,C,D 四种型号共500套,B型号公租房的入住率为40%.A,B,C,D 四种型号竣工的套数及入住的情况绘制了图1和图2两幅尚不完整的统计图. 
(1)请你将图1和图2的统计图补充完整;
(2)在安置中,由于D型号公租房很受欢迎,入住率很高,2012年竣工的D型公租房中,仅有5套没有入住,其中有两套在同一单元同一楼层,其余3套在不同的单元不同的楼层.老王和老张分别从5套中各任抽1套,用树状图或列表法求出老王和老张住在同一单元同一楼层的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N. 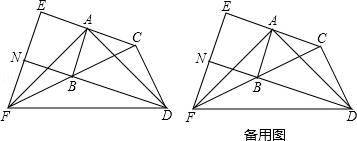
(1)求证:AD=AF;
(2)试判断四边形ABNE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣ ![]() ;⑤2a<b+
;⑤2a<b+ ![]() ,正确的是( )
,正确的是( )
A.①③
B.①②③
C.①②③⑤
D.①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com