
【题目】“校园安全”受到全社会的广泛关注,绵阳市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: 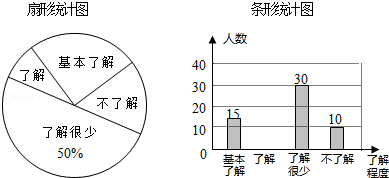
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若该中学共有学生3000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
【答案】
(1)60;90°
(2)解:60﹣15﹣30﹣10=5;
补全条形统计图得:

(3)解:根据题意得:3000× ![]() =1000(人),
=1000(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为1000人
(4)解:画树状图得:

∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,
∴恰好抽到1个男生和1个女生的概率为: ![]() =
= ![]()
【解析】解:(1)∵了解很少的有30人,占50%, ∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为: ![]() ×360°=90°;
×360°=90°;
所以答案是:60,90°;
【考点精析】解答此题的关键在于理解扇形统计图的相关知识,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况,以及对条形统计图的理解,了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两校派相同人数的优秀学生,参加县教育局举办的中小学生美文诵读决赛。比赛结束后,发现学生成绩分别是7分、8分、9分或10分(满分10分),核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料,请你回答下列问题:
甲校成绩统计表 | ||||
成绩 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 | |
(1)在图①中,“7分”所在扇形的圆心角等于_______
(2)求图②中,“8分”的人数,并请你将该统计图补充完整。


(3)经计算,乙校学生成绩的平均数是8.3分,中位数是8分。请你计算甲校学生成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好?
(4)如果教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据解答过程填空(理由或数学式)
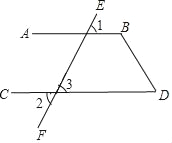
如图,已知∠1=∠2,∠D=60°,求∠B的度数.
解∵∠2=∠3( )
又∵∠1=∠2(已知),
∴∠3=∠1(等量代换)
∴ ∥ ( )
∴∠D+∠B=180°( )
又∵∠D=60°(已知),
∴∠B= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,当顶角A的大小确定时,它的对边BC与邻边(腰AB或AC)的比值确定,记为f(A),易得f(60°)=1.若α是等腰三角形的顶角,则f(α)的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,E在AB上,且∠DCE=67.5°,DE⊥AB于E,若AE=1,线段BE的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.
![]()
(1)请写出线段AB中点M表示的数是 .
(2)现有一只蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇.
①求A、B两点间的距离;
②求两只蚂蚁在数轴上的点C相遇时所用的时间;
③求点C对应的数是多少?
(3)若蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左运动,同时另一只蚂蚁恰好从A点出发,以每秒2个单位长度的速度沿数轴也向左运动,设两只蚂蚁在数轴上的D点相遇,求D点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个形状、大小完全相同的含有30゜和60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
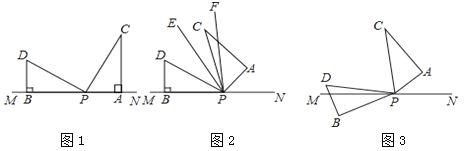
(1)试说明:∠DPC=90゜;
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动),以下两个结论:①![]() 为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发
的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路
以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距
离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
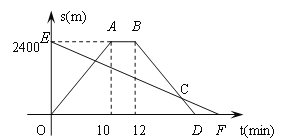
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com