
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N. 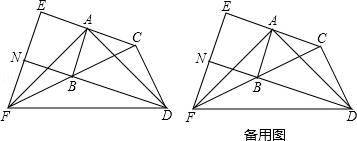
(1)求证:AD=AF;
(2)试判断四边形ABNE的形状,并说明理由.
【答案】
(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
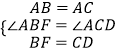 ,
,
∴△ABF≌△ACD(SAS),
∴AD=AF
(2)解:四边形ABNE是正方形;理由如下:
证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中, 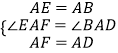 ,
,
∴△AEF≌△ABD△AEF≌△ABD(SAS),
∴BD=EF;
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
∵∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形
【解析】(1)由等腰直角三角形的性质得出∠ABC=∠ACB=45°,求出∠ABF=135°,∠ABF=∠ACD,证出BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;(2)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
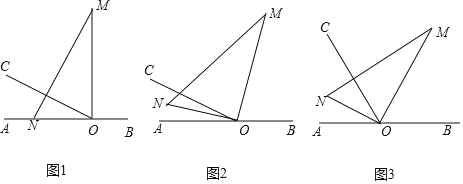
【题目】如图1,两个形状、大小完全相同的含有30゜和60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
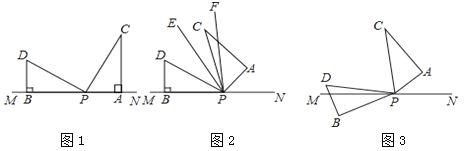
(1)试说明:∠DPC=90゜;
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动),以下两个结论:①![]() 为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发
的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路
以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距
离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
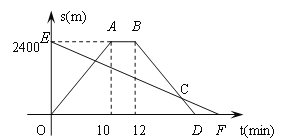
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后OM恰好平分∠BOC,则t= (直接写结果)
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多少秒后OC平分∠MON?请说明理由;
(3)在(2)问的基础上,那么经过多少秒∠MOC=36°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④4a﹣2b+c>0,其中正确的个数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是一个“数值转换机”(箭头为数进入转换机的路径,方框是对进入的数进行转换的转换机).
(1)当输入7、-2018这两个数时,求出它们各自输出的结果;

(2)若输入一非零数,其输出结果为0,则输入的数是多少?(找一个即可)
(3)若输出的结果是2,请直接写出输入的数.(用含自然数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式![]() x+y+1的值.
x+y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.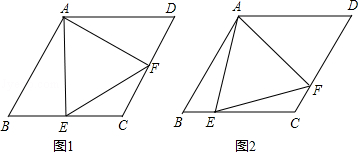
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过 秒钟两人第一次相遇;若两人同时出发,同向而行,则经过 秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com