
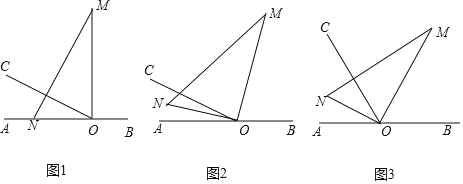
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC=30������һֱ�����ǰ壨��M=30������ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
(1)��ͼ1�е����ǰ��Ƶ�O��ÿ��3�����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ2������t���OMǡ��ƽ�֡�BOC����t=�� ����ֱ��д�����
(2)��(1)�ʵĻ����ϣ������ǰ���ת����ͬʱ������OCҲ��O����ÿ��6�����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ3����ô�����������OCƽ�֡�MON����˵�����ɣ�
(3)��(2)�ʵĻ����ϣ���ô�����������MOC=36������˵�����ɣ�
���𰸡���1��5����2��5��ʱOCƽ����MON�����������������3���������.
��������
��1���������̼��ɽ�����⣻
��2��������MOC=45��������������⼴�ɣ�
��3�����ݡ�AON+��BOM=90������BOC=��COM�����AONΪ3t����AOCΪ30��+6t���ٸ��������г�������⼴��.
��1���١ߡ�AON+��BOM=90�㣬��COM=��MOB��
�ߡ�AOC=30�㣬
���BOC=2��COM=150�㣬
���COM=75�㣬
���CON=15�㣬
���AON=��AOC����CON=30�㩁15��=15�㣬
��ã�t=15���3��=5�룻
���ǣ��������£�
�ߡ�CON=15�㣬��AON=15�㣬
��ONƽ����AOC��
��2��5��ʱOCƽ����MON���������£�
�ߡ�AON+��BOM=90�㣬��CON=��COM��
�ߡ�MON=90�㣬
���CON=��COM=45�㣬
�����ǰ��Ƶ�O��ÿ��3�����ٶȣ�����OCҲ��O����ÿ��6�����ٶ���ת��
����AONΪ3t����AOCΪ30��+6t��
�ߡ�AOC����AON=45�㣬
�ɵã�6t��3t=15�㣬
��ã�t=5�룻
��3������ͼ��OCƽ����MOB
�ߡ�AON+��BOM=90�㣬��BOC=��COM��
�����ǰ��Ƶ�O��ÿ��3�����ٶȣ�����OCҲ��O����ÿ��6�����ٶ���ת��
����AONΪ3t����AOCΪ30��+6t��
���COMΪ![]() ��90�㩁3t����
��90�㩁3t����
�ߡ�BOM+��AON=90�㣬
�ɵã�180�㩁��30��+6t��=![]() ��90�㩁3t����
��90�㩁3t����
��ã�t=![]() �룻
�룻
�𣺾���![]() ����MOC=36�㣮
����MOC=36�㣮


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
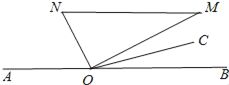
����Ŀ����ͼ����֪��ABC�͡�DEF����E��BC���ϣ���A��DE���ϣ���EF�ͱ�AC�ཻ�ڵ�G�����AE=EC����AEG=��B����ô��������һ�������������ж���DEF���ABCһ�����Ƶ��ǣ� �� 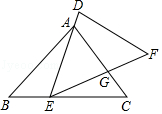
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϋ�������ϵľ���ԼΪ210km��С������С�γ���С�ſ��Ŵ����������Ϋ��ȥ���ϣ�С����С��������1Сʱ���������ͬʱ������ϣ���֪С�γ����ٶ��Ǵ�����ٶȵ�1.5����
��1����С�γ��ʹ�������ٶȸ��Ƕ��٣����з��̽��
��2����С������ʱ����С������ϻ��ж�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
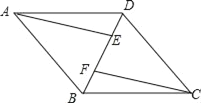
����Ŀ����֪����ͼ���ı���ABCD��ƽ���ı��Σ�AE��CF���ҷֱԽ���BD�ڵ�E��F��
��1����֤����AEB�ա�CFD��
��2������AF��CE������AFE=��CFE����֤���ı���AFCE�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�й��ⷿ��������ע��2012�꿢���Ĺ��ⷿ��A��B��C��D �����ͺŹ�500�ף�B�ͺŹ��ⷿ����ס��Ϊ40%��A��B��C��D �����ͺſ�������������ס�����������ͼ1��ͼ2�����в�������ͳ��ͼ�� 
��1�����㽫ͼ1��ͼ2��ͳ��ͼ����������
��2���ڰ����У�����D�ͺŹ��ⷿ���ܻ�ӭ����ס�ʺܸߣ�2012�꿢����D���ⷿ�У�����5��û����ס��������������ͬһ��Ԫͬһ¥�㣬����3���ڲ�ͬ�ĵ�Ԫ��ͬ��¥�㣮���������ŷֱ��5���и��γ�1�ף�����״ͼ���б����������������ס��ͬһ��Ԫͬһ¥��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ϣ���ʦ����������⣺ ��ͼ1�������������ֽƬABC��BC��AC�����������۵����õ���AB��BC��CA�ϵĵ�D��E��F��ʹ���ı���DECFǡ��Ϊ���Σ�
С�����۵��������£�
��ͼ2����1��AC����BC���۵���ʹAC������BC���ϣ��õ��ۺ۽�AB��D�� ��2��C����AB���۵���ʹC����D���غϣ��õ��ۺ۽�BC����E����AC����F��
��ʦ˵����С����������ȷ����
��ش�С�������۵��������� �� 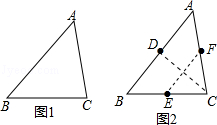
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�͡�BCD�У���BAC=��BCD=90�㣬AB=AC��CB=CD���ӳ�CA����E��ʹAE=AC���ӳ�CB����F��ʹBF=BC������AD��AF��DF��EF���ӳ�DB��EF�ڵ�N�� 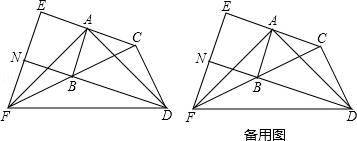
��1����֤��AD=AF��
��2�����ж��ı���ABNE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����������x���ཻ��A��B���㣬�䶥��P������C��D��E���ƶ�������C��D��E������ֱ�Ϊ����1��4������3��4������3��1������B�ĺ��������СֵΪ1�����A�ĺ���������ֵΪ�� ��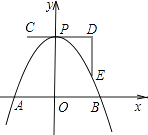
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˼����С����̽������ֱ�ߵ�λ�ù�ϵ��������ʱ�������ˡ��д������Ρ��������������ഹֱ�������γ�Ϊ���д������Ρ�����ͼ��1����ͼ��2����ͼ��3���У�AM��BN�ǡ�ABC�����ߣ�AM��BN�ڵ�P�����ABC�����������ξ�Ϊ���д������Ρ�����BC=a��AC=b��AB=c��
��1����ͼ1����tan��PAB=1��c=4 ![]() ʱ��a= �� b=��
ʱ��a= �� b=��
��ͼ2������PAB=30�㣬c=2ʱ��a= �� b=��
��2������۲죨1���еļ�����������a2��b2��c2����֮��Ĺ�ϵ���õ�ʽ��ʾ������������ͼ3֤����Ľ��ۣ�
��3����ͼ4��ABCD�У�E��F�ֱ���AD��BC�����ȷֵ㣬��AD=3AE��BC=3BF������AF��BE��CE����BE��CE��E��AF��BE�ཻ��G��AD=3 ![]() ��AB=3����AF�ij���
��AB=3����AF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com