
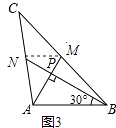
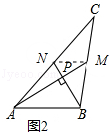
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
【答案】
(1)4 ![]() ;4
;4 ![]() ;
;![]() ;
;![]()
(2)
解:结论a2+b2=5c2.
证明:如图3中,连接MN.
∵AM、BN是中线,
∴MN∥AB,MN= ![]() AB,
AB,
∴△MPN∽△APB,
∴ ![]() =
= ![]() =
= ![]() ,
,
设MP=x,NP=y,则AP=2x,BP=2y,
∴a2=BC2=4BM2=4(MP2+BP2)=4x2+16y2,
b2=AC2=4AN2=4(PN2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2
(3)
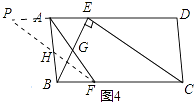
解:如图4中,在△AGE和△FGB中,
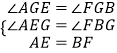 ,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF= ![]() AD=
AD= ![]() ,
,
∴9+AF2=5×( ![]() )2,
)2,
∴AF=4.
【解析】(1)解:如图1中,∵CN=AN,CM=BM,
∴MN∥AB,MN= ![]() AB=2
AB=2 ![]() ,
,
∵tan∠PAB=1,
∴∠PAB=∠PBA=∠PNM=∠PMN=45°,
∴PN=PM=2,PB=PA=4,
∴AN=BM= ![]() =2
=2 ![]() .
.
∴b=AC=2AN=4 ![]() ,a=BC=4
,a=BC=4 ![]() .
.
故答案为4 ![]() ,4
,4 ![]() ,
,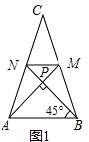
如图2中,连接NM,
, ∵CN=AN,CM=BM,
∴MN∥AB,MN= ![]() AB=1,
AB=1,
∵∠PAB=30°,
∴PB=1,PA= ![]() ,
,
在RT△MNP中,∵∠NMP=∠PAB=30°,
∴PN= ![]() ,PM=
,PM= ![]() ,
,
∴AN= ![]() ,BM=
,BM= ![]() ,
,
∴a=BC=2BM= ![]() ,b=AC=2AN=
,b=AC=2AN= ![]() ,
,
故答案分别为 ![]() ,
, ![]() .
.
(1)①首先证明△APB,△PEF都是等腰直角三角形,求出PA、PB、PN、PM,再利用勾股定理即可解决问题.②连接MN,在RT△PAB,RT△PMN中,利用30°性质求出PA、PB、PN、PM,再利用勾股定理即可解决问题.(2)结论a2+b2=5c2 . 设MP=x,NP=y,则AP=2x,BP=2y,利用勾股定理分别求出a2、b2、c2即可解决问题.(3)取AB中点H,连接FH并且延长交DA的延长线于P点,首先证明△ABF是中垂三角形,利用(2)中结论列出方程即可解决问题.


科目:初中数学 来源: 题型:
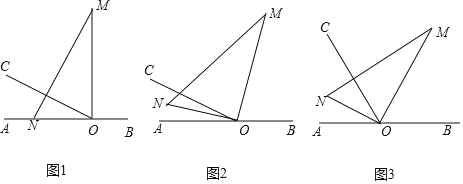
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后OM恰好平分∠BOC,则t= (直接写结果)
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多少秒后OC平分∠MON?请说明理由;
(3)在(2)问的基础上,那么经过多少秒∠MOC=36°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.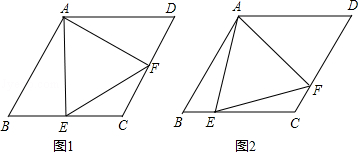
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在河的两岸有A,B两个村庄,河宽为4千米,A、B两村庄的直线距离 AB=10千米,A、B两村庄到河岸的距离分别为1千米、3千米,计划在河上修建一座桥MN垂直于两岸,M点为靠近A村庄的河岸上一点,求AM+BN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. 
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 经过第一象限的点
经过第一象限的点![]() 和点
和点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 的面积为
的面积为![]() .
.
![]() 求
求![]() 点的坐标;
点的坐标;
![]() 求直线
求直线![]() 的函数表达式;
的函数表达式;
![]() 直线
直线![]() 经过线段
经过线段![]() 上一点
上一点![]() (
(![]() 不与
不与![]() 、
、![]() 重合),求
重合),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过 秒钟两人第一次相遇;若两人同时出发,同向而行,则经过 秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
查看答案和解析>>
科目:初中数学 来源: 题型:
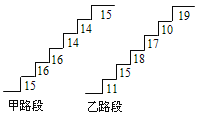
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com