
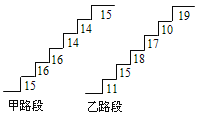
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
【答案】(1)甲台阶高度的平均数15,乙台阶高度的平均数15;(2)甲段路走起来更舒服一些;(3)游客行走更舒服.
【解析】(1)根据图中所给的数据,利用平均数公式求解即可;
(2)根据平均数、中位数、方差和极差的特征回答即可;
(3)结合方差,要使台阶路走起来更舒服,就得让方差变得更小,据此提出合理性的整修建议.
(1)甲台阶高度的平均数:(15+16+16+14+14+15)÷6=15,
乙台阶高度的平均数:(11+15+18+17+10+19)÷6=15.
(2)甲段路走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数)使得方差为0,游客行走更舒服.


科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )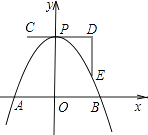
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米. 
(1)分别求隧道AC和BC段的长度;
(2)建工集团安排甲、乙两个金牌施工队分别从隧道两头向中间施工,甲队负责AC段施工,乙队负责BC段施工,乙每天的工作量是甲的2倍,两队同时开工5天后,甲队将速度提高25%,乙队将速度提高了150%,从而两队同时完成,求原计划甲、乙两队每天各施工多少米.(参考数据:tan23°≈0.4,cos23°≈0.9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.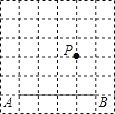
(1)在图甲中画出一个ABCD.
(2)在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(![]() 年—
年—![]() 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元![]() 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为![]() 、
、![]() 、
、![]() ,则三角形的面积
,则三角形的面积![]() (公式里的
(公式里的![]() 为半周长即周长的一半).
为半周长即周长的一半).
请利用海伦一秦九韶公式解决以下问题:
(![]() )三边长分别为
)三边长分别为![]() 、
、![]() 、
、![]() 的三角形面积为__________.
的三角形面积为__________.
(![]() )四边形
)四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 的面积为__________.
的面积为__________.
(![]() )五边形
)五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,五边形
,五边形![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x>0时,反比例函数 ![]() ( )
( )
A.图象在第四象限,y随x的增大而增大
B.图象在第三象限,y随x的增大而增大
C.图象在第二象限,y随x的增大而减小
D.图象在第一象限,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com