
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.
(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为______________;
(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
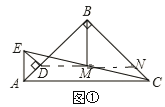

【答案】BD=![]() BM
BM
【解析】(1)根据等腰直角三角形的性质,根据“直角三角形斜边上的中线等于斜边的一半”可知BD=![]() BM;
BM;
(2)先证明△MDE≌△MFC,得出AD=ED=FC,再作AN⊥EC于点N,证出△DBF是等腰直角三角形,根据点M是DF的中点,得出△BMD是等腰直角三角形,即可得出BD=![]() BM.
BM.
(1)∵∠ABC=∠ADE=90°,
∴ED∥BC,
∴∠DEM=∠MCB,
在△EMD和△CMN中
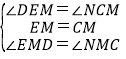
∴△EMD≌△CMN(ASA),
∴CN=DE=DA,MN=MD,
∵BA=BC,
∴BD=BN,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,∠DBM=![]() ∠DBN=45°=∠BDM,
∠DBN=45°=∠BDM,
∴△BMD为等腰直角三角形.
∴BD=![]() BM,
BM,
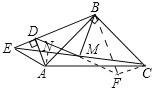
(2)结论成立.
证明:过点C作CF∥ED,与DM的延长线交于点F,连接BF,
可证得△MDE≌△MFC,
∴DM=FM,DE=FC,
∴AD=ED=FC,
作AN⊥EC于点N,
由已知∠ADE=90°,∠ABC=90°,
可证得∠DEN=∠DAN,∠NAB=∠BCM,
∵CF∥ED,
∴∠DEN=∠FCM,
∴∠BCF=∠BCM+∠FCM=∠NAB+∠DEN=∠NAB+∠DAN=∠BAD,
∴△BCF≌△BAD,
∴BF=BD,∠DBA=∠CBF,
∴∠DBF=∠DBA+∠ABF=∠CBF+∠ABF=∠ABC=90°,
∴△DBF是等腰直角三角形,
∵点M是DF的中点,
则△BMD是等腰直角三角形,
∴BD=![]() BM.
BM.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
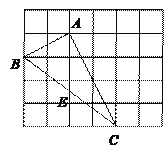
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为_______,CD的长为______,AD的长为________;
(3)四边形ABCD的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2+bx﹣3经过点A(7,﹣3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
(1)求m的值;
(2)求这条抛物线的表达式;
(3)点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.4).
=2.4).
查看答案和解析>>
科目:初中数学 来源: 题型:
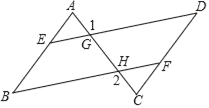
【题目】在括号内注明说理依据.如图已知∠B=∠D,∠1=∠2,试猜想∠A与∠C的大小关系,并说明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代换)
∴AB∥CD
∴∠A=∠C .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
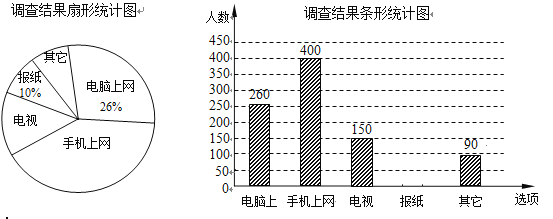
根据以上信息解答下列问题:
(1)这次抽样调查的样本容量是 ;
(2)通过“电视”了解新闻的人数占被调查人数的百分比为 ;扇形统计图中, “手机上网”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有70万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com